wyznacz
Mania: Punkty A(−2,−1) oraz D(2,2) są wierzchołkami rombu, którego przekątna AC jest zawarta w prostej
o równaniu x−3y−1=0. Wyznacz współrzędne pozostałych wierzchołków tego rombu. Wykonaj obrazek
pomocniczy.
15 maj 15:03
Maciess:
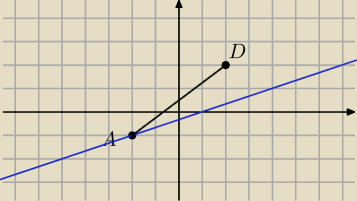
15 maj 15:35
Maciess: Prosta AC w postaci kierunkowej
Romb, czyli prosta BD będzie do niej prostopadła
y=−3x+b przechodzi przez D więc wstawiamy współrzędne i otrzymuje
b=8 y=−3x+8
Wyznaczamy punkt przecięcia przekątnych
−9x+24=x−1
x=2.5 ⇒ y=0.5 S=(2.5 , 0.5) −− punkt przecięcia się przekątnych
B=(x
B,−3x
B+8)
x
B=3 y
B=−1
B=(3,−1)
Spróbuj w ten sam sposób doliczyć punkt C
15 maj 15:54
jc: Przekątne mają wspólny środek.
C=B+D−A = (3,−1) + (2,2) + (−2,−1) = (3, 0)
15 maj 16:14
jc: Maciess, teraz wypatrzyłem, że powyżej znalazłeś środek.
Po co przekształcasz równanie prostej?
x−3y=1
Prosta prostopadła przechodząca przez (2,2):
3x+y=3*2+2=8
Przecięcie: S=(5/2, 1/2)
15 maj 16:20
Maciess: Nie wiem, zawsze zadanka robiłem na postaci kierunkowej, ale widze trzeba się będzie przeprosić
z ogólną.
15 maj 16:33
