Geometria Arab: Znaleźć pkt symetryczny do punktu A=(−2;9) względem prostej l: 2x−3y+18=0

ABC: poprowadź prostopadła przez ten punkt i znajdź punkt przecięcia a potem ze wzoru na środek odcinka

Leszek: Napisz rownanie prostej prostopadlej do l : 2x −3y +18=0 i przechodzacej przez A , Wyznacz punkt przeciecia tych prostych S , jest to srodek odcinka AB , i znajdziesz B .

Arab:

	3
to tak rownanie p.prostopadlej to będzie y= −		+6, pkt przecięcia prostych S(0,6) a A'
	2

wyjdzie (2,3) tak ?

janek191: Ma być

	3
y = −		x + 12
	2

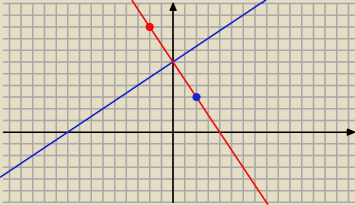
janek191: Pomyłka:

	3
y = −		x + 6
	2

Arab:

	3
Teraz zgłupiałem to ma być .... +12 i pomyłka to y=−		+6 czy jednak pomyłka u cb i ma
	2

być tak jak ja napisałem

janek191: Dobrze 20.06

janek191: Dlaczego gubisz x ?

Arab: Oj, przez te pisanie ułamka U '{}{}"

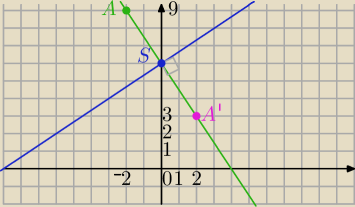
Mila: II sposób− równania prostych w postaci ogólnej. A=(−2;9) względem prostej l: 2x−3y+18=0 1) prosta prostopadła do l i przechodząca przez A=(−2,9) m⊥l m: 3x+2y+C=0 i 3*(−2)+2*9+C=0 c=−12 m: 3x+2y−12=0 2) S− Punkt przecięcia prostych 3x+2y−12=0 /*3 2x−3y+18=0 /*2 9x+6y−36=0 4x−6y+36=0 5x=0, x=0 i y=6 S=(0,6)− środek AA' A=(−2,9),A'=(x,y)

	−2+x		9+y
0=		, 6=
	2		2

x=2 i y=3 A'=(2,3) ====== Albo A' wyznaczymy wektorowo AS^→=[2,−3] S=(0,6)→T_[2,−3]⇒A'=(0+2, 6−3)=(2,3) ================

Eta: bastet zmienił nick na Arab