prostokąt tomek: Na bokach AB i AD prostokąta ABCD wybrano odpowiednio punkty M i N tak że trójkąt CMN jest równoboczny. Wykaż,ze suma pól trójkątów BMC i DNC jest równa polu trójkąta MAN

jc: Przyjmijmy długość boku środkowego trójkąta równą 4. pole jednego z mniejszych trójkątów = 2 sin a cos a = sin 2a, drugi trójkąt ma pole sin 2(30−a), a trzeci sin 2(30+a) Wystarczy teraz sprawdzić tożsamość: sin 2(30+a) = sin 2a + sin 2(30−1) lub inaczej: sin t = sin (t+60) + sin(t−60). Na pewno istniej jakiś rysunkowy dowód. Szukaj.

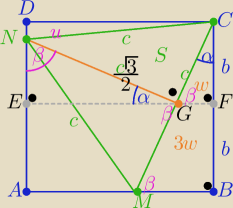
Eta: 1/ rys. zgodny z treścią zad. 2/ odpowiednie oznaczenia ( zgodne z treścią 3/|NG|=hΔMNC = c√3/2 odcinek EF || AB przechodzi przez środki boków AD i BC i G∊EF i α+β=90^o

	c√3
4/ΔBMC podobny do ENG z cechy (kkk) w skali k=		= √3/2 to k2=3/4
	2c

	1
zatem P(ENG)=3w i P(BMC)=4w to P(FGC)=		P(BMC)=w
	4

to P(ENG)=P(BMGF)=3w p(NGC)=s = P(MGN) i P(DNC)=u i P(MAN)=x i mamy w prostokącie EFCD: P₁▭=4w+s+u w prostokącie ABFE : P₂▭= 3w+s+x−3w ⇒ P₂▭= x+s P ₁=P₂ ⇒ x+s=4w+s+u ⇒ x = 4w+u czyli P(MAN)=P(BMC)+P(DNC) ===================== c.n.w.

Mila:

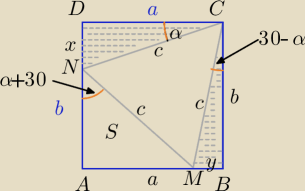
	1
1)P1= PΔDNC+PΔBMC=		*(x*a+y*b)
	2

	x
sinα=		⇔x=c*sinα, a= c*cosα
	c

	y
sin(30−α)=		, y=c*sin(30−α), b=c*cos(30−α)
	c

	1
P1=		*[c*sinα*c*cosα+c*sin(30−α)*c*cos(30−α)]
	2

	1		1
P1=		c2*[		sin2α+sin(30−α)*cos(30−α)]=
	2		2

	1		1		1
=		c2*(		sin2α+		(sin(60−2α)]=
	2		2		2

	1		2α+60−2α		2α−60+2α
=		c2*2*sin		*cos		=
	4		2		2

	1		1
=		c2*sin30*cos(2α−30)=		c2*cos(2α−30)
	2		4

	1
2) PΔMAN=		*|AN|*|AM|
	2

|AN|=c*cos(α+30), |AM|=c*sin(α+30)

	1		1
PΔMAN=		c2*sin(α+30)*cos(α+30)=		c2sin(2α+60)
	2		4

sin(2α+60)=cos(90−2α−60)=cos(−2α+30)=cos(2α−30)⇔ P_ΔDNC+P_ΔBMC= P_ΔMAN cnw Trzeba pomyśleć nad sposobem bez trygonometrii.

Mila: O, witaj Eto, napisałaś bez tryg. I JC też dał wskazówkę. Miałam przerwę w pisaniu i nie widziałam wpisów

Eta: