Planimetria Leviane : W trójkącie równoramiennym podstawa ma długość a i jest dwa razy krótsza od każdego z boków. Oblicz stosunek pól figur, na jakie dzieli ten trójkąt symetralna jednego z ramion. Ma ktoś może pomysł jak zrobić to zadanie prowadząc środkowe zamiast obliczać tangens?

Leszek: Z twierdzenia cosinusow oblicz cos α miedzy ramionami i nastepnie w gornym trojkacie prostokatnym oblicz z funkcji trygonometrycznej bok Koniecnie zrob rysunek !

Leszek: Wynik to 2/5

Leviane : Dziękuję!

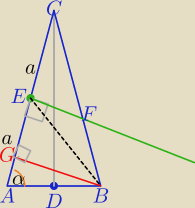
Mila: Bez trygonometrii. |AB|=a, |A|=|BC|=2a P_ΔABC=P 1) EB − środkowa

	1
PΔABE=PΔEBC=		P
	2

PΔEFC		|CF|
	=
PΔEFB		|FB|

	GA		AD		AG		1   a 2
2) ΔABG∼ΔADC⇔		=		⇔		=
	AB		AC		a		2a

	1
|AG|=		a
	4

=====

	3
|GE|=		a
	4

3) GB||EF Z tw.Talesa:

CE		CF		a		CF		CF		4
	=		⇔		=		⇔		=		⇔
EG		FB		3   a 4		FB		FB		3

P_ΔEFC=4s i P_ΔEFB=3s

	1		P
4s+3s=		P⇔s=
	2		14

	4P		2
PΔEFC==		=		P
	14		7

	5
PABFE=		P
	7

PΔEFC		2
	=
PABFE		5

=======================