rozniczkowanie rozniczkowanie: 1) Czy ciąg stały jest ciągiem Cauchy'ego? Wydaje mi się, że tak. 2) Czy szereg i ciąg sum częściowych to, to samo? Do tej pory myślałam, że to są inne pojęcia. I że w szeregach po prostu korzystamy pomocniczo z ciągu sum częściowych. 3) Czy zbiór zwarty (domknięty i ograniczony) może nie przyjmować swoich kresów? 4) Czy można różniczkować funkcję na zbiorze domkniętym? (robiliśmy to tylko na otwartych) 5) Czy pochodna może zerować się na początku lub końcu przedziału, i czy możemy tam mieć ekstremum lokalne? 6) Jeżeli funkcja jest klas C^∞ to wszystkie pochodne muszą być ciągłe, aby móc liczyć kolejną pochodną, zgadza się? Pozdrawiam i z góry bardzo dziękuję za odpowiedzi.

ABC: Ad 1 −tak Ad 2− według pewnych książek tak Ad 3− pytanie chyba źle sformułowane, ciągły obraz zbioru zwartego jest zwarty ale nie wiem czy o to chodziło , ponadto w przestrzeniach euklidesowych z naturalną topologią zwartość to to samo co domkniętość i ograniczoność

rozniczkowanie: @ABC! Bardzo Ci dziękuję Mógłby ktoś wypowiedzieć się na pozostałe pytania?

rozniczkowanie: do 3) Funkcja ciągła przyjmuje na każdym podzbiorze zwartym swoje kresy, tzn. jeżeli f: R−> R, a ograniczymy ją do f: [−1,1]−>R, to chodzi o to, że wartość najmniejsza oraz największa w tej nowej dziedzinie, funkcja będzie osiągała, ponieważ dziedzina to zbiór domknięty. Tak?

wredulus_pospolitus: 4) można ... w końcu np dla f(x) = (√x)³ i D_f = [0;+∞) wyznaczamy pochodną wzór pochodnej dla całej dziedziny 5) nie bardzo rozumiem pytanie ... chodzi Ci w momencie w którym rozpatrujesz przedział domknięty [a,b] i f'(a) = 0 bądź f'(b) = 0 Jeżeli D_f = [a,b] to tak, funkcja może (a nawet będzie miała − bo nie ma możliwości wystąpienia punktu przegięcia) ekstremum lokalne 6) ... ciągła 'w swojej dziedzinie' i posiada ona NIEZEROWE pochodne w końcu f(x) = 1 będzie miała ciągłe pochodne (równe 0), a nie jest C^∞

wredulus_pospolitus: 20:32 −−− tak

ABC: co do 20:32 tak, ciągła funkcja rzeczywista określona na zbiorze domkniętym i ograniczonym osiąga swoje kresy

Adamm: 4) W punktach skupienia, jak najbardziej. 5) Dla funkcji określonej na przedziale [a, b] zerowanie się pochodnej w punktach a czy b nic tak naprawdę nie oznacza. Może tak być, ale nic to nie zmienia. 6) tak, skoro istnieje pochodna rzędu n+1, to pochodna rzędu n musi być ciągła

wredulus_pospolitus: Adamm nie zgodzę się co do (5) ... zerowanie się pochodnej na krańcu (powiedzmy f(a) = 0) oznacza, że mamy jedną z sytuacji: I) ∃_c>a ∀_xn∊(a,c) −> f(a) ≥ f(x_n) II) I) ∃_c>a ∀_xn∊(a,c) −> f(a) ≤ f(x_n) o ile pochodna nie jest stale stała 0 w tym otoczeniu to nierówności będą ostre i mamy minimum bądź maksimum lokalne

wredulus_pospolitus: Jeszcze raz: I) ∃_c>a ∀_xn∊(a,c) f(a) ≥ f(x_n) II) ∃_c>a ∀_xn∊(a,c) f(a) ≤ f(x_n)

wredulus_pospolitus: w sumie to już to oznacza że w punkcie a mamy ekstremum lokalne

Adamm: przy założeniu że pochodna jest ciągła

Adamm: 'o ile pochodna nie jest stale stała 0 w tym otoczeniu to nierówności będą ostre i mamy minimum bądź maksimum lokalne' hmm... to że stale nie jest równa zeru, nie oznacza że nie zmienia znaku nieskończenie wiele razy w otoczeniu lewego punktu

wredulus_pospolitus: sam fakt, że mamy f(a) = 0 oraz ∃_c>0 ∀_xn∊(a,c) f'(x_n) ≠ 0 oznacza, że w tym przedziale zachodzi tylko jedno z f(a) > f(x_n) lub f(a) < f(x_n) a jako, że dla x<a funkcja nie jest określona to w punkcie x=a nie możemy mieć punktu przegięcia. Ale tak jak wcześniej napisałem ... nie muszą być ostre nierówności, aby mówić o ekstremum lokalnym.

wredulus_pospolitus: A jeżeli rozpatrujemy takie funkcje, które mają nieskończenie wiele ekstrem w otoczeniu punku a (np. f(x) = sin(1/x) dla x>0 i 'cokolwiek' dla x=0), to wtedy niestety funkcja ta nie będzie ciągła − przynajmniej ja tak to widzę.

rozniczkowanie: 5) Mam takie tw. Niech f: [a,b]−>R. Jeżeli f ma w x₀ ∊(a,b) maksimum/minimum lokalne oraz f'(x₀) istnieje, to f'(x₀)=0. Nie rozumiem dlaczego, x₀ nie może być ze zbioru [a,b].

rozniczkowanie: Chodzi o to, co napisał @Adam? Że to nic nie zmieni?

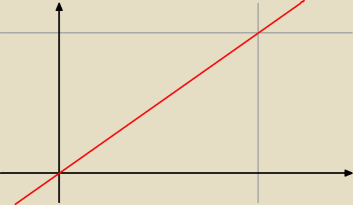
Adamm: Np. f(x) = x, x∊[0, 1] Ta funkcja ma ekstrema lokalne w punktach 0 i 1 ale f'(x) = 1 ≠ 0 dla każdego x Dlatego założenia że x jest z (a, b) nie można ulepszyć

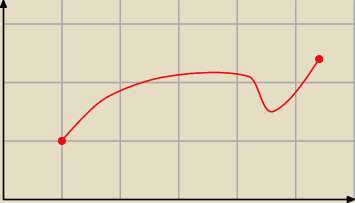
wredulus_pospolitus: to że masz minimum/maksimum lokalne na krańcu NIE OZNACZA że w tym miejscu masz f'(a) = 0 Zauważ, że zarówno 'a' jak i 'b' są (odpowiednio) minimum i maksimum lokalnym tejże funkcji (baa ... nawet są minimum/maksimum globalnym), ale ... ale f'(a) ≠ 0 oraz f'(b) ≠ 0 ... a czemuż to? Odpowiedź: Bo patrząc na ciągłą funkcję określoną na przedziale domkniętym krańce przedziałów (czyli a i b) będą minium/maksimum lokalnym (zawsze i wszędzie)

ICSP: Aby funkcja miała minimum/maksimum lokalne w punkcie x₀ musi istnieć pewne otoczenie punktu x₀ w którym ta funkcja jest określona. Dlatego funkcja na krańcach dziedziny nie może mieć ekstremum.

jc: Jeśli całym światem jest odcinek [0,1], to otoczeniem punktu 0 jest odcinek [0,a), 0<a<1. W taki wypadku można przecież mówić o ekstremum w w punkcie 0, choć to kraniec odcinka, a że takiego ekstremum nie odkryjemy przyrównując pochodną do zera, to już inna sprawa.

rozniczkowanie: Myślałam, że f'(x)=0, jest warunkiem koniecznym (nieważne, w którym miejscu odcinka punkt x leży), aby w tym x było ekstremum lokalne, ale widocznie byłam w błędzie. Bardzo dziękuję za pomoc!

rozniczkowanie: f: [a,b]−>R Jeszcze raz dla pewności: zerowanie się pochodnej w punkcie x jest warunkiem koniecznym, aby mieć ekstremum lokalne, jeżeli punkt x należy do (a,b)?

rozniczkowanie: plus co jeśli mamy f:(a,b)−> R. czy reszta tw pozostaje bez zmian?

Bleee: Tak i tak (pozostaje bez zmian). Problemem są krańce przedziałów ze względów które napisaliśmy powyżej.