kury zielononóżki iteRacj@: sympatyczne zadanie ze szkoły podstawowej Kura szukająca robaków chodzi na obu nogach, kura zamyślona stoi na jednej nodze, drugiej nie widać. Jeśli kura siedzi na grzędzie, to wcale nie widać jej nóg. W gospodarstwie jest 99 kur, ale widzimy sto ich nóg. Dwa razy więcej kur stoi i chodzi niż wdrapało się na grzędę. Ile jest kur, które chodzą?

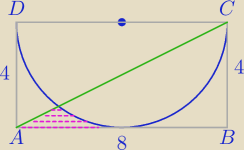
Mila: Zadanie 2 . Rozwiąż równanie w zbiorze liczb całkowitych: 615+x²=2^y Zadanie 3. oblicz pole zacieniowanej figury:

kogut: 1/ chodzą −−ch , stoją na jednej nodze −−s , siedzą na grzędzie −−g 34 ch −− 68 nóg 32 s −− 32 nóg −−−−−−−−−−−−−−− 66 kur −− 100 n to 66:2= 33 g razem mamy 99 kur Odp: 34 kurki chodzą i zbierają robaczki

Mariusz: Zadanie 3. Czyżby rachunek całkowy ? Zadanie 2. 615=2^y−x² Niech y=2k (2^2k−x²)=615 (2^k−x)(2^k+x)=615 (2^k−x)(2^k+x)=5*123 (64−59)(64+59)=5*123 (y = 12) ⋀ (x = 59 ⋁ x = −59)

Mariusz: Niech A = (0,0) C = (8,4) Równanie prostej zawierającej odcinek AC

	4−0
y=		(x−0)
	8−0

	1
y=		x
	2

Równanie okręgu (x−4)²+(y−4)²=16

	1
(x−4)2+(		x−4)2=16
	2

	1
x2−8x+		x2−4x+16=0
	4

5
	x2−12x+16=0
4

5x²−48x+64=0

48±√2304−1280
10

48±32
10

x₂=8 x₁=1.6

	1		1
∫01.6		xdx+∫1.64.0		x−(4−√16−(x−4)2)dx
	2		2

(y−4)²=16−(x−4)² y − 4=−√16−(x−4)² y = 4−√16−(x−4)²

	1		1
∫01.6		xdx+∫1.64.0		x−(4−√16−(x−4)2)dx
	2		2

1
	x2|01.6=0.64
4

	−(x−4)2
∫√16−(x−4)2dx=(x−4)√16−(x−4)2−∫
	√16−(x−4)2

∫√16−(x−4)²dx=(x−4)√16−(x−4)²−U{16−(x−4)²−16}{√16−(x−4)²dx

	1
∫√16−(x−4)2dx=(x−4)√16−(x−4)2−∫√16−(x−4)2dx+16∫		dx
	4√1−((x−4)/4)2

	x−4
2∫√16−(x−4)2dx=(x−4)√16−(x−4)2+16arcsin(		)
	4

	1		x−4
∫√16−(x−4)2dx=		(x−4)√16−(x−4)2+8arcsin(		)
	2		4

1		1		x−4
	x2−4x+		(x−4)√16−(x−4)2+8arcsin(		)|1.64
4		2		4

(4−16+0+0)−((0.64−6.4)−3.84−8arcsin(0.6)) −12−0.64+10.24+8arcsin(0.6) −2.4+8arcsin(0.6) P = 0.64 −2.4+8arcsin(0.6) P = −1.76 + 8arcsin(0.6) Tyle wyszło całką ale może błędnie napisałem całkę oznaczoną

Mariusz: Chyba nie to pole policzyłem

	1
∫01.6		xdx+∫1.64(4−√16−(x−4)2)dx
	2

1
	x2|016=0.64
4

	1		x−4
∫1.64(4−√16−(x−4)2)dx=4x−		(x−4)√16−(x−4)2−8arcsin(		)|1.64
	2		4

(16−0−0)−(6.4+3.84+8arcsin(0.6)) 5.76−8arcsin(0.6) P = 0.64+5.76−8arcsin(0.6) P = 6.4 − 8arcsin(0.6)

iteRacj@: I masz ten samy wynik co Presh Talwalkar.

Mariusz: A co do tego trzeciego zadania to 1. Czy aby na pewno dobrą całkę napisałem ? 2. Czy dałoby radę obliczyć to pole bez całki ? Pierwsza część to pole trójkąta prostokątnego i nie trzeba całki a jak policzyć drugą część pola bez całki ?

iteRacj@: https://www.youtube.com/watch?v=2Seb863FnfU Jedno rozwiązanie z użyciem całek i drugie oparte na trygonometrii + jak zawsze przekonywujący Presh Talwalkar.

Mila: To były zadania dla licealisty, zapomniałam napisać. Mariusz bez całki policzyłam. Nic się nie chcą uczyć. Dawniej tak nie było, co się dzieje z młodzieżą?

Maciess: Po maturach lekkie rozluźnienie po całorocznej gonitwie za zaległościami. Ja robiłem w ten sam sposób jak pan Talwalkar. Całka tutaj to chyba ta przysłowiowa "armata"

Mila: To zabieraj się do analizy Maciess, o ile idziesz na studia z matematyką. Co planujesz?

Maciess: Zadanie 2. Jak cos takiego rozwiązywać? Ja robiłem tak x i y muszą być dodatnie Lewa strona musi potęgą dwójki wiec szukam w kolejnych potęgach dwójki pomniejszonych o 615 wartosci którą da się spierwiastkować. x=59 y=12

Maciess: Milu planuje matematyke na studia własnie, ale ciągle siedzi w głowie obawa ze nie mam tego talentu i odpadne. No ale pewnie spróbuje i waham sie teraz między uniwerkiem a politechniką.

ABC: Maciess nie masz pojęcia jakie egzemplarze skończyły matematykę więc się nie obawiaj

Mila: Zadanie 2) Prawa jest liczbą parzystą. Teraz wypisz kilka wartości dla lewej strony, musisz coś zauważyć. np. dla x∊{1,2,3,4,5} Wtedy napisz co zauważyłeś?

Mariusz: Mila ale w jaki sposób policzyć to bez całki Maciess zapomniałeś jeszcze o ujemnej

Mila: ABC zależy na jakiej uczelni

Maciess: Jesli x jest parzyste, to lewa strona jest nieparzysta. Wniosek taki, że x musi byc nieparzyste

Mila: Poczekaj Mariusz, jeśli licealiści nie napiszą rozwiązania, to ja napiszę. Podpowiedź: Liczę pole trójkąta krzywoliniowego o wierzchołku b potem pole odcinka koła.

Maciess: Mariusz fakt, parzysta potęga

Mariusz: Sama matematyka niewiele daje Jak ktoś lubi matematykę to może lepiej coś powiązanego z matematyką jak informatyka czy może ekonomia

Mila: MasiessJeszcze zauważ jakie liczby otrzymujesz , gdy podstawiasz x nieparzyste.

Mila: Informatyka jest trudniejsza niż matematyka, ale można znaleźć atrakcyjną pracę. Wszystkie trudności można pokonać, ale trzeba włożyć dużo pracy własnej.

Maciess: Kiedy nieparzyste, to cała lewa strona jest parzysta tak jak napisałem. Nie widze nic więcej

Mila: 615+1=616 615+9=624 615+25=640 liczby te są podzielne przez 4. Równanie może mieć rozwiązanie jeżeli prawą stronę przedstawimy w postaci: 2^y, gdzie y=2n 615+x²=2²ⁿ⇔ (*) x²−2²ⁿ=615 615=1*3*5*41 Rozłóż ze wzoru skróconego mnożenia lewą stronę równania (*) i teraz kombinuj.

Maciess: (2ⁿ−x)(2ⁿ+x)=5*123 y=12 i x=59 lub x=−59 W ten sposob trzeba sobie radzić. To taki standardowy sposob rozwiązywania/analizy takich rownan czy do kazdego trzeba podchodzić indywidualnie?

Ckegn: @Mila gdzie informatyka trudna ja mialem szustke z niej zmatematyki zaś czwurke z polskiego zaś... nawet nie powiem:(

Mila: Tak można rozwiązać pewne typy zadań, ale trzeba rozpisać wszystkie przypadki. Podobne: Rozwiąż w zbiorze liczb całkowitych. x²−y²=63

Mila: Widzę, [N[CKE...}} że język polski mało zgłębiałeś. Mówisz o studiach informatycznych , czy nauce w LO?

Ckegn: niewiem nie pamietam juz dokladnie no ale tworzenie folderuw, pisanie w wordzie excel itp proscizna sama a matematyka juz trudna polski tez

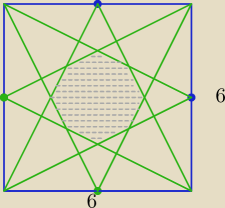
Mila: Zadanie 4. Oblicz pole ośmiokąta .

t: coto wgle jest

Maciess: (x−y)(x+y)=63 63=1*3²*7 x=12 y=9 x=−12 y=−9 x=−12 y=9 x=12 y=−9 x=32 y=31 x=−32 y=−31 x=32 y=−31 x=−32 y=31 x=8 y=1 x=−8 y=−1 x=8 y=−1 x=−8 y=1

Maciess: Mam pomysł na osmiokąt ale juz dopisze jutro. Na szybko to w srodku kwadrat i wykazac podobienstwo trojkatow.

Mariusz: Może udałoby się przyjąć jakiś układ współrzędnych, wyznaczyć punkty przecięcia prostych zawierających boki trójkątów Policzyć pola trójkątów np wyznacznikami i spróbować tak odjąć aby otrzymać pole tego ośmiokąta

Mariusz: Zauważyliście to że w analizie całką pojedynczą można obliczyć pole a podwójną objętość natomiast w algebrze wyznacznikiem drugiego stopnia można policzyć pole a wyznacznikiem trzeciego stopnia można policzyć objętość