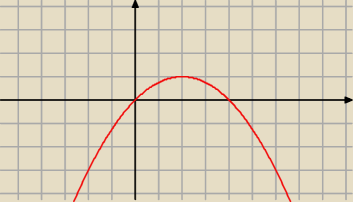
 a) f(x) = a x2 + b x + c
W = ( 2, 1)
więc
f(x) = a*(x − 2)2 + 1
oraz f(3) = 0 ⇒ a*( 0 − 2)2 + 1 = 0
4 a + 1 = 0
4 a = − 1
a = −0,25
dlatego
f(x) = − 0,25*(x − 2)2 + 1 = − 0,25*( x2 − 4 x + 4) + 1 = − 0,25 x2 + x
a = − 0,25
b = 1
c = 0
a) f(x) = a x2 + b x + c
W = ( 2, 1)
więc
f(x) = a*(x − 2)2 + 1
oraz f(3) = 0 ⇒ a*( 0 − 2)2 + 1 = 0
4 a + 1 = 0
4 a = − 1
a = −0,25
dlatego
f(x) = − 0,25*(x − 2)2 + 1 = − 0,25*( x2 − 4 x + 4) + 1 = − 0,25 x2 + x
a = − 0,25
b = 1
c = 0
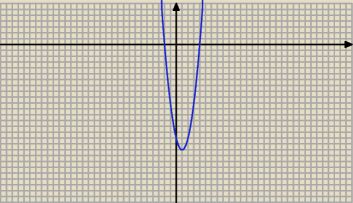 b) f(x) = a x2 + b x + c
x1 = −2 x2 = 4 f(0) = 16
więc
f(x) = a*( x + 2)*( x − 4)
oraz
f(0) = 16 ⇒ a*(0+2)*(0 − 4) = 16
− 8 a = 16
a = 2
wiec
f(x) = 2*( x + 2)*(x − 4) = 2*( x2 − 4 x + 2 x − 8) = 2 x2 −4 x − 16
a = 2 b = − 4 c = − 16
====================
b) f(x) = a x2 + b x + c
x1 = −2 x2 = 4 f(0) = 16
więc
f(x) = a*( x + 2)*( x − 4)
oraz
f(0) = 16 ⇒ a*(0+2)*(0 − 4) = 16
− 8 a = 16
a = 2
wiec
f(x) = 2*( x + 2)*(x − 4) = 2*( x2 − 4 x + 2 x − 8) = 2 x2 −4 x − 16
a = 2 b = − 4 c = − 16
====================
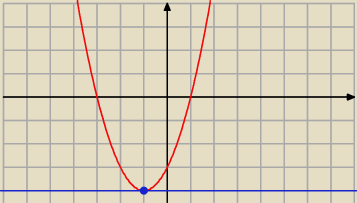 c) x1 = −3 x2 = 1 Równanie stycznej y = − 4 ⇒ q = − 4
Mamy
c) x1 = −3 x2 = 1 Równanie stycznej y = − 4 ⇒ q = − 4
Mamy
| − 3 + 1 | ||
p = | = − 1 | |
| 2 |
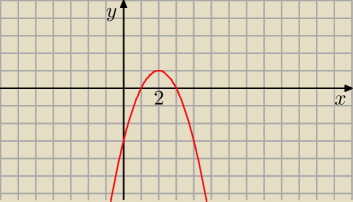 Poprawka − 16.20
Tam powinno być:
f(3) = 0 ⇒ a*(3 − 2)2 + 1 = 0
a + 1 = 0
a = − 1
więc
f(x) = − 1*(x − 2)2 + 1 = − ( x2 − 4 x + 4) + 1 = − x2 + 4 x − 3
a = − 1 b = 4 c = − 3
=======================
Poprawka − 16.20
Tam powinno być:
f(3) = 0 ⇒ a*(3 − 2)2 + 1 = 0
a + 1 = 0
a = − 1
więc
f(x) = − 1*(x − 2)2 + 1 = − ( x2 − 4 x + 4) + 1 = − x2 + 4 x − 3
a = − 1 b = 4 c = − 3
=======================