kwadrat Love: Rozszerzenie Niech A będzie wierzchołkiem kwadratu, a M środkiem przeciwległego boku. Na przekątnej kwadratu wychodzącej z wierzchołka A wybrano punkt P tak, aby |AP| = |MP|. Obliczyć, w jakim stosunku punkt P dzieli przekatną kwadratu.

PW: Plan rozwiązania metodami geometrii analitycznej Niech kwadrat ma bok o długości 2 (dla ułatwienia rachunków, niezależnie od długości boku proporcje odcinków sa takie same). Umieśćmy ten kwadrat w układzie współrzędnych, tak by A = (0, 0) i boki były rówoległe do osi układu, M = (2, 1). Równanie prostej AM ma postać

	x
(1) y =		.
	2

Punkt P leży na symetralnej odcinka AM. Umiemy napisać równanie tej symetralnej (prosta prostopadła do prostej (1), przechodząca przez środek odcinka AM). Niech równanie symetralnej ma postać (2) − sam napisz jak ono wygląda) Punkt P leży również na prostej zawierającej przekątną kwadratu, to znaczy na prostej (3) y = x. Układ równań (2) i (3) daje współrzędne punktu P. Liczymy |AP|, długość przekątnej (2√2) i stosunek |AP| do 2√2−|AP|.

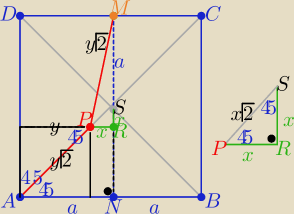
Eta: |RN|=y=a−x , x∊(0,a) ,|AP|=y√2=(a−x)√2 i |PC|=|PS|+|SC|= x√2=a√2= (a+x)√2 to

|AP|		a−x
	=
|PC|		a+x

w ΔRMP : |RM|=a+x , |PR|=x , |PM|=|AP|=(a−x)√2 z tw. Pitagorasa [(a−x)√2]²=x²+(a+x)² ⇒ ............ a²−6ax=0 /: a≠0 to 6x=a zatem:

|AP|		6x−x		5
	=		=
|PC|		6x+x		7

|AP| : |PC|=5 :7 =============

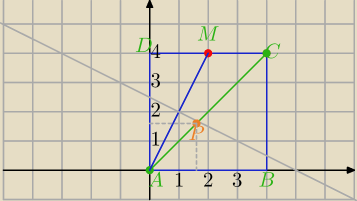
Mila: Punkt P leży na przecięciu prostej AC i symetralnej AM A=(0,0), M=(2,4) 1) prosta AM m: y=2x c: y=x prosta AC 2) Symetralna AM S=(1,2) − środek AM

	1		5
s: y=−		x+
	2		2

3) Punkt przecięcia prostych :

	1		5
y=x i y=−		x+
	2		2

	5		5
x=		, y=
	3		3

4)

	5
|AP|=		√2
	3

	5		7
|PC|=4√2−		√2=		√2
	3		3

AP		5
	=
PC		7

============