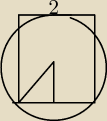
 1.Dany jest kwadrat o boku 2. Na podstawie rysunku oblicz promień okręgu
2.Przedstaw wyrażenie w postaci iloczynu 4−x2+2xy−y2
3.Sprawdz czy liczby a=(sin60+cos60)2 i b=sin215−cos30+cos2!5
są pierwiastkami wielomianu W(x)=4x3−8x2+x
1.Dany jest kwadrat o boku 2. Na podstawie rysunku oblicz promień okręgu
2.Przedstaw wyrażenie w postaci iloczynu 4−x2+2xy−y2
3.Sprawdz czy liczby a=(sin60+cos60)2 i b=sin215−cos30+cos2!5
są pierwiastkami wielomianu W(x)=4x3−8x2+x
| 1 | ||
promien okregu opisanego na kwadracie: r = | d gdzie d = a√2 | |
| 2 |
| 1 | ||
r = | d = √2 | |
| 2 |
| √3 | 1 | √3+1 | ||||
sin60 + cos60 = | + | = | ||||
| 2 | 2 | 2 |
| √3+1 | 3+2√3+1 | 4+2√3 | √3 | |||||
( | )2 = | = | = 1+ | |||||
| 2 | 4 | 4 | 2 |
| √3 | √3 | √3 | √3 | |||||
W(1+ | ) = 4(1+ | )3 − 8(1+ | )2 + 1+ | = | ||||
| 2 | 2 | 2 | 2 |
| √3 | √3 | √3 | ||||
(1+ | )(4(1+ | )2 − 8*(1+ | ) +1) = | |||
| 2 | 2 | 2 |
| √3 | 3 | |||
(1+ | )(4*(1+√3 + | ) − 8 − 4√3 +1) = | ||
| 2 | 4 |
| √3 | ||
(1+ | )(4 + 4√3 + 3 −8 −4√3+1) = | |
| 2 |
| √3 | ||
(1+ | ) * 0 = 0 czyli ta liczba jest pierwiastkiem wielomianu | |
| 2 |
| √3 | ||
b=sin215 − cos30 + cos215 = 1 − | ||
| 2 |
| √3 | √3 | √3 | √3 | |||||
W(1 − | ) = (1 − | )(4*(1 − | )2 − 8*(1 − | ) +1) = | ||||
| 2 | 2 | 2 | 2 |
| √3 | 3 | |||
(1 − | ) (4(1−√3+ | ) − 8 +4√3 +1) = | ||
| 2 | 4 |
| √3 | √3 | |||
(1 − | ) (4 −4√3 +3 −8+4√3+1) = (1 − | )*0 = 0 czyli ta liczba tez jest | ||
| 2 | 2 |
