pochodna, a styczna pochodna: Jaki jest związek między pochodną, a styczną? Czy pochodną w punkcie funkcji, może interpretować, jako styczną do niej w tym punkcie?

janek191: To jest współczynnik kierunkowy stycznej.

wredulus_pospolitus: albo jak wolisz (to znaczy to samo co janek napisał): wartość pochodnej funkcji f(x) w punkcie x_o jest równy tangensowi kąta stycznej z osią OX

pochodna: @janek191, dzięki! A może coś jeszcze powiedzieć o związku między pochodną, a styczną? Czy wyłącznie współczynnik kierunkowy?

pochodna: A więc przy funckji y=|x| w punkcie x=0, nie mamy pochodnej, ponieważ nie można poprowadzić w tym punkcie stycznej?

wredulus_pospolitus: nie ... styczną można poprowadzić i to nie jedną ... problem jest własnie to i to nie jedną

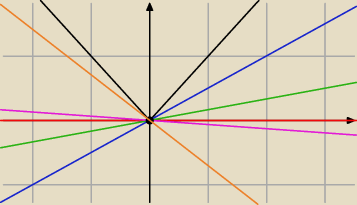
wredulus_pospolitus: każda z tych kolorowych prostych jest styczną do f(x) = |x| w punkcie x_o = 0

mat: Nie no, nie ma stycznej w 0 tak jak napisał pochodna

mat: Oj chyba nie do końca tak jest

wredulus_pospolitus: mat ... STYCZNA (a raczej styczne) do wykresu f(x) = |x| istnieje (patrz definicja stycznej), ale pochodna nie istnieje ponieważ ów stycznych jest więcej niż jedna

mat: Tzn dla mnie nie ma sensu o mówienie o stycznej w odosobnionym punkcie (0,0). Zawsze bierzemy pewien fragment krzywej która go zawiera

wredulus_pospolitus: Nie bardzo Ciebie teraz rozumiem o co Ci chodzi.

mat: Szukając stycznej w punkcie (0,0) powinienem wziąć kawałek (otoczenie) wykresu y=|x| z prawej i lewej

wredulus_pospolitus: Dobra ... przyznaję się − jeżeli się wybierze definicję stycznej, która DOBRZE opisuje kwestię stycznej (a nie jak się to 'potocznie' określa) to faktycznie f(x) = |x| nie posiada stycznej. Jako ciekawostkę podam, że f(x) = √|x| będzie posiadała styczną w punkcie x_o = 0, a pochodnej w tymże punkcie (oczywiście) nie będzie.

wredulus_pospolitus: Heh ... całe życie inaczej 'podchodziłem' do kwestii stycznej

Satan: Fragment? Myślałem, że styczna i funkcja mają dokładnie jeden punkt wspólny. Też chętnie się dowiem, o co chodzi

Satan: Macie Panowie definicję?

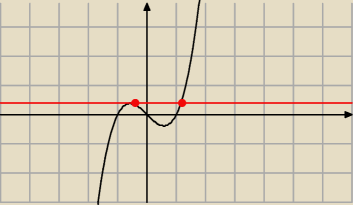
wredulus_pospolitus: masz przykład f(x) = x(x²−1) ... styczna w x_o = −1 ma więcej niż jeden punkt wspólny z f(x)

wredulus_pospolitus: innym przykładem jest KAŻDA funkcja liniowa, ponieważ styczna do tej funkcji, będzie właśnie tą funkcją

wredulus_pospolitus: styczna (wedle definicji) jest funkcją graniczną siecznych wykresu f(x) przechodzących przez x_o oraz x (gdzie x−> x_o)

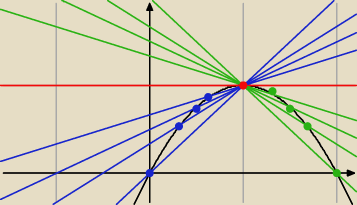
wredulus_pospolitus: a więc: