geometria analityczna 00000:

	−1		1		1		1
Punkty A=(		, −1		), B=(3		,		) są wierzchołkami trójkąta równoramiennego
	2		2		2		2

ABC o podstawie AB. Ramię BC zawiera się w prostej o równaniu 8x+14y−35=0. Oblicz współrzędne punktu C i pole tego trójkąta. Czy mógłby mi ktoś podpowiedzieć jakie obliczenia należy wykonać, aby obliczyć dane punktu C?

PW: Na przykład tak: Punkt C należy do prostej, która jest prostopadła do AB i przechodzi przez środek AB (to znaczy znajdujemy równanie symetralnej boku AB). C należy również do prostej o równaniu 8x+14y−35 = 0. Rozwiązujemy układ równań.

Mila:

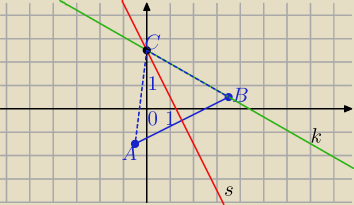
	1		3		1		1
A=(−		,−		), B=(3		,		)
	2		2		2		2

8x+14y−35=0⇔

	4		5
1)k: y=−		x+
	7		2

2) Symetralna AB

	1		3		7		1
(x+		)2+(y+		)2=(x−		)2+(y−		)2⇔
	2		2		2		2

	5
s: y=−2x+
	2

2) C− Punkt przecięcia prostych k i s

	5		4		5
−2x+		=−		x+
	2		7		2

	4
−2x=−		x
	7

	5
x=0 ,y=
	2

	5
C=(0,
	2

3) Pole Δ: AB^→=[4,2]

	1
AC→=[		,4]
	2

W: 4 2

1
	4
2

	1
W=4*4−2*		=15
	2

	1		7
P=		*15=
	2		2

============

00000: Dziękuję!