planimetra angelika: W trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC. Wykaż, że prawdziwa jest równość | BC|² −|AC|² = |AB| ⋅|AC| .

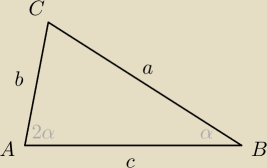
Pytający: z tw. sinusów mamy, że

a		b
	=
sin2α		sinα

a		b
	=
2sinαcosα		sinα

2bsinαcosα=asinα

	a
cosα=
	2b

z tw. cosinusów b²=a²+c²−2ac•cosα

	a
b2=a2+c2−2ac•
	2b

	a2c
a2−b2=		−c2
	b

a²b−b³=a²c−bc² a²b−a²c−b³+bc²=0 a²(b−c)−b(b²−c²) =0 a²(b−c)−b(b−c)(b+c)=0 (b−c)(a²−b²−bc)=0 b=c lub a²−b²=bc

angelika: bardzo dziękuję matura blisko