Optymalizacja przedmaturalna Alvinek: Nie wychodzi mi to zadanko a nie wiem gdzie robię błąd. Jeżeli jest ktoś w stanie pomóc będę wdzięczny Rozpatrujemy wszystkie trójkąty obwodzie L i jednym kącie o mierze 120 stopni. Oblicz długości boków trójkąta, dla którego pole koła wpisanego w ten trójkąt będzie największe. Zacząłem od tego że oznaczając sobie boki przy kącie 120 a oraz b obliczam pole trójkąta i dostaję taką zależność: ab=4√3/3 P_trójkąta Następnie z twierdzenia cosinusów dla boku c(naprzeciwko kąta 120) otrzymuję że P_trójkąta=(3L²−6Lc)/4*√3 Następnie ze wzoru r=2P/L obliczam r i wstawiam do wzoru na polę koła. Tylko że dostaję w tym wzorze funkcję i dodatnim współczynniku przy c a szukamy wartości największej. Dziedzina to c∊(0;L/2) więc też nie pomaga. Wiem że to epopeja ale jeżeli faktycznie ktoś może pomóc przed maturą byłbym wdzięczny

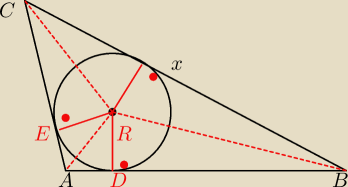
an: CB=x ∡CAB=120^o

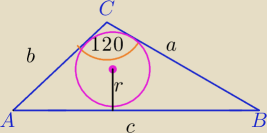
Mila: wg mnie powinien wyjść Δ równoramienny 1) a+b+c=L

	1		ab√3
PΔ=		ab*sin120=
	2		4

lub

	L
P=		*r stąd r:
	2

	2P
r=
	L

Mianownik ma stałą wartość, Wartość ułamka jest największa , jeśli pole Δ jest największe. 2) c²=a²+b²+ab z tw. cosinusów c=√a²+b²+ab z (1) a+b=L−c ⇔a+b=L−√a²+b²+ab , ⇔ p{a²+b²+ab)=L−(a+b) /², L>a+b a²+b²+ab=L²−2L(a+b)+a²+2ab+b² 0=L²−2La−2Lb+ab 2L*b−ab=L²−2La b*(2L−a)=L²−2La

	L2−2La		L
b=		, a<
	2L−a		2

3)

	√3		L2−2L*a
P(a)=		*a*
	4		2L−a

	2L(a2−4La+L2)
P'(a)=
	(2L−a)2

analizuj pochodną a=2L−√3L b=2L−√3L c=... Taką masz odpowiedź?

Alvinek: No tak jest dobrze i odpowiedź się zgadza tylko zastanawiałem się czemu z mojej metody przy wyznaczaniu c jako parametru nie wychodziło a nie widziałem błędu

Mila: c jest zmienną zależną od a i b, to dlatego. Pewnie jest inny sposób, ale na razie nie widzę.

Alvinek: Jest inny sposób na kątach jak masz ochotę to możesz podziałać no cóż dziękuję bardzo liczę że nie będzie takich problemów w czwartek

Mila: To za trudne na maturę.

Alvinek: Rozszerzoną?

Mila: Myślę, że byłyby kłopoty. Przecież tu są maturzyści na forum i nie rozwiązywali. Może ktoś jeszcze zabierze się za to zadanie.

Alvinek: Teoretycznie rzecz biorąc nie ma tu nic poza meteriał ale patrząc na optymalizacje we wcześniejszych latach to faktycznie były bardziej intuicyjne

an:

	√3
h=x
	2

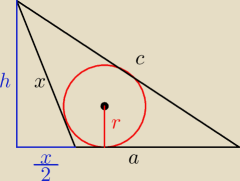
	x		2lx−l2
h2+(		+a)=c2 c2=(l−a−x)2 ⇒a=
	2		x−2l

	√3		2x2−lx
S={ah}{2}=		l
	4		x−2l

	2S		√3l	2x2−lx		√3		2x2−lx
r=		=2			=		*
	l		4l	x−2l		2		x−2l

	√3		(4x−l)(x−2l)−2lx2+lx
r'=		*
	2		(x−2l)2

x²−4lx +l²=0 x₁=l(2−√3) x₂=l(2+√3) odrzucamy gdyż nie może być x>l

	2lx−l2
a=		=l(2−√3)
	x−2l

c=2√3−3l