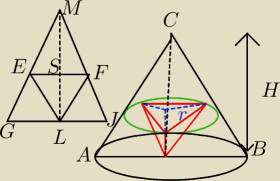
stereometria salv: Dany jest stożek o wysokości 6 i promieniu podstawy 3.W stożek ten wpisano ostrosłup prawdiłowy trójkątny w ten sposób,że wysokość ostrosłupa jest zawarta w wysokości stożka,wierzchołek ostrosłupa jest środkiem podstawy,a wierzchołki podstawy ostrosłupa należą do powierzchni bocznej stożka.Oblicz największą możliwą objętość takiego ostrosłupa. Zrobiłem dosyć z automatu te zadanie i wynik wyszedł dobry,ale teraz im dłużej się zastanawiam tym bardziej nie wiem.

	a√3
Narysowałem ten przekrój (w lewym górnym rogu),oznaczając,że SF=SE to		,
	3

|ML|=6,|MS|=6−h,|GL|=|LJ|=3 no i z podobieństwa,potem wzór na objętość pochodna i wyszło,ale jak wygląda ten przekrój w rysunku przestrzennym tym po prawej?

iteRacj@: Ten przekrój po lewej nie jest prawidłowo narysowany. Tak może wyglądać przekrój, gdy wpisany ostrosłup ma w podstawie np. sześciokąt foremny. Rysunek po prawej jest OK.

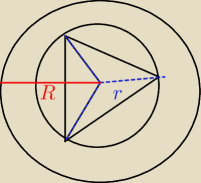salv: Takie coś mi jeszcze świta..ale jak to będzie wyglądać z boku?

iteRacj@: Widok z góry jest dokładnie taki. A jak to będzie wyglądać przekrój płaszczyzną prostopadłą do podstawy, zależy od tego, przez jakie punkty będzie przechodzić płaszczyzna, która wyznaczy przekrój.

iteRacj@: Na przekroju z lewej:

	2		a√3		1		a√3
jeżeli |SF|=		*		, to |SE|=		*		(lub na odwrót)
	3		2		3		2