Matura pikus: W trójkącie ABC dane są podstawa |AB| = a, kąt ostry przy podstawie CAB = 2α i dwusieczna tego kąta |AD| = d. Obliczyć pole koła opisanego na tym trójkącie. Podać warunek istnienia rozwiązania.

pikus: Obliczylem sam. Juz nie trzeba

pikus: To ktoś inny napisał to nie ja nadal trzeba

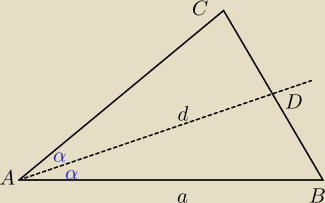
iteRacj@: z tw. cosinusów dla ΔADB wylicz długość odcinka DB z tw. sinusów dla ΔADB oblicz miarę kąta <CBA z sumy kątów w ΔABC oblicz miarę kąta <ACB z tw. sinusów dla ΔABC wylicz promień koła opisanego na tym trójkącie

pikus: Dzięki a jak podać warunek istnienia rozwiązania?

pikus: Up

iteRacj@: Bez obliczeń nie umiem odpowiedzieć, a nie jestem teraz w stanie liczyć tego promienia.

pikus: Czyli BD=√a²+d²−2adcosα

	dsinα
sin<CBA=
	BD

Wiec

	a*BD
R=
	2dsinα

Jeśli wszysko jest ok, to jaki jest warunek istnienia rozwiązania?

Mila: Z jakiej proporcji obliczyłeś R?

pikus: sory

	dsinα
R= a/[ 2sin(2α+arcsin(		)]
	BD

Chyba już ok? Ale jaki jest warunek istnienia rozwiązania?

Mila: 1) sinβ, |DB| mam tak, jak u Ciebie. 2) obliczyłam b=|AC| tak:

1		1		1
	a*b*sin(2α)=		b*d*sinα+		*d*a*sinα
2		2		2

stąd 2ab*cosα=b*d+ad

	ad
b=
	2a*cosα−d

2a*cosα−d>0 2a cosα>d

	d
cosα>
	2a

	d
0<		<1
	2a

b
	=2R
sinβ

podstawić za b.

pikus: Czyli takie warunki jak napisałaś to jest właśnie warunek rozwiazywalnosci zadania?

Mila: Do mojego rozwiązania chyba tak. U Ciebie

	dsinα
0<		<1
	BD

Nie masz odpowiedzi do zadania? Skąd to zadanie?

Mila: Poprosimy Etę, aby podała swój wynik, o ile pojawi się na forum

pikus: Nie mam odpowiedzi