W ostrosłupie prawidłowym czworokątnym... XZ: Proszę o POMOC! W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są do siebie prostopadłe. a) oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy. b) Jakim procentem objętości sześcianu, którego krawędź ma długość równą długości krawędzi podstawy danego ostrosłupa, jest objętość tego ostrosłupa?

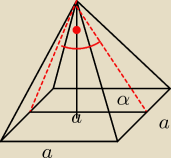
Godzio: jest to trójkąt prostokątny równoramienny więc a=h√2

	h		√2
sinα=		=
	a		2

Godzio: b) α=45

	H		1
tg45 =		=		a = H
	1   a 2		2

1   a2H 3		1   a3 6
	*100% =		* 100% = 16,6%
a3		a3

XZ: A czasem kąt alfa nie będzie gdzie indziej? Bo to jest między krawędzią podstawy a płaszczyzną podstawy.

Godzio: zawsze tak samo

XZ:

	√3
Kurczę, ale mimo wszystko w odpowiedziach jest inaczej, jest
	3

XZ: Ale nie przejmuj się, dzięki Twojej pomocy, wyszło mi jak miło wyjść xD Dzięki