ostrosłup Michał: Podstawą ostrosłupa ABCDS jest trapez ABCD . Przekątna AC tego trapezu ma długość 8√3 , jest prostopadła do ramienia BC i tworzy z dłuższą podstawą AB tego trapezu kąt o mierze 30 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 4√5 . Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej SD . czy z tego wynika że na podstawie ABCD można opisać okrąg a spodek wysokości ostrosłupa jest w połowie dłuższej podstawy?

Michał: Nie wyjaśnione Proszę o odpowiedź, ktoś się podszywa

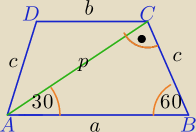
Mila: Wszystkie krawędzie boczne są równe, to znaczy ,że spodek wysokości ostrosłupa leży w środku okręgu opisanego na trapezie, w takim razie trapez jest równoramienny, jako wpisany w okrąg. Okrąg opisany na trapezie jest jednocześnie opisany na ΔABC, który jest Δprostokatnym. Środek tego okręgu znajduje się w środku AB ( przeciwprostokątna ΔABC). Dalej dasz radę?

Michał: oczywiście dziękuję