geometria analityczna
salv:
Dany jest trójkąt ABC o polu równym 5,gdzie A=(5,3) B=(1,0).Prosta zawierająca wysokość
trójkąta ABC ma równanie y=2x−7.Wyznacz współrzędne punktu C.
D(x,2x−7)
Czyli wysokość opada z wierzchołka A,bo na leży do tej prostej.
No to licze:
|BD|
2+|DA|
2=|AB|
2
(x−1)
2+(2x−7)
2+(5−x)
2+(10−2x)
2=25
x=3,x=5
D(3,−1),D=(5,3)−>odpada bo to współrzędne punktu A, S(4,1)
Czy do tego momentu nie ma błędu?Chciałem potem zapisać współrzędne punktu C w postaci takiej
jak punktu D poprzez wyznaczanie prostej prostopadlej do prostej y=2x−7 przechodzacej przez
punkt B i opisać okrąg na trójkącie ADC i skorzystać z faktu,że |SD|=|SC|
3 maj 15:31
salv: dobra jednak nie,zapatrzylem sie i punkt S jest źle wyznaczony bo to środek przeciwprostokatnej
ma byc

3 maj 15:33
Maciess: Wyznacz sobie prostą prostopadła do wysokości z A i przechodzącej przez punkt B i masz prosta
która zawiera C.
Potem mozesz liczyc pole z uzyciem wyznacznika pary wektorow.
3 maj 15:39
salv: wiem,ze sa takie wzory ale wole zrobić tak,jakby ich nie było

3 maj 15:43
Maciess: Dlaczego? Ten wzór jest w karcie nawet. I to zadanie wtedy na prawde wymaga mniej liczenia
3 maj 15:44
salv: tak,to prawda może to dziwnie zabrzmi ale wole się nie przyzwyczajać do niektórych wzorów
których używa się na dobrą sprawę bardzo rzadko(przynajmniej ja mam takie odczucie) i poszukać
jakichś zależności innych

3 maj 15:47
Maciess: Bardzo dziwne podejście, ale twoja wola

3 maj 15:59
Mila:
Obliczyłeś bez wyznacznika?
3 maj 18:48
salv: Nie,chcialem tylko wiedziec czy do momentu wyznaczenia punktu D wszystko jest ok
3 maj 19:24
salv: | | 1 | | 1 | |
wyszło mi równanie tożsamościowe po obliczeniu środka AC C(x,− |
| x+ |
| ) i |SC|=|SA| |
| | 2 | | 2 | |
3 maj 19:32
Mila:
D=(3,−1)
3 maj 20:34
Mila:
To co, liczyć?
3 maj 20:35
salv: Tak,poprosiłbym

3 maj 20:38
Mila:
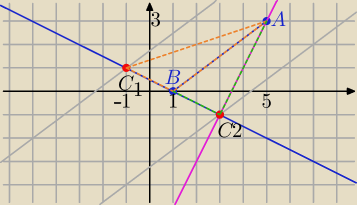
A=(5,3), B=(1,0)
1) k: y=2x−7 prosta zawierająca wysokość opuszczoną na bok BC
|AB|=5
| 1 | |
| |AB|*h=5⇔h=2 dł. wysokości opuszczonej na bok AB |
| 2 | |
2)
równanie prostej BC, BC⊥k
| | −1 | | 1 | |
a: y= |
| x+b i B ∊a⇔b= |
| ⇔ |
| | 2 | | 2 | |
3) Punkt C leży na przecięciu prostej równoległej do AB odległej od niej o 2 i prostej BC.
a) prosta AB:
b) Prosta równoległa do AB:
Odległość 2 jednostki od prostej AB
|−3/4−b'|=2*
√1+9/16
| 3 | | 5 | | 3 | | 5 | |
| +b'= |
| lub |
| +b'=− |
| |
| 4 | | 2 | | 4 | | 2 | |
| | 3 | | 7 | | 1 | | 1 | |
c) Punkt przecięcia |
| x+ |
| =− |
| x+ |
| |
| | 4 | | 4 | | 2 | | 2 | |
C
1=(−1, 1)
lub
C
2=(3,−1)
Mamy dwa trójkąty.
Policz teraz z wyznacznika, jeśli znowu nie wyjdzie, to policzę.
Sprawdź, czy odległość c jest właściwa.
3 maj 21:36
salv: Wyszło to samo, bardzo dziękuję

3 maj 21:53
Mila:
W którym sposobie mniej obliczeń?
3 maj 22:11
salv: W wyznaczniku, ale chciałem też znać inny sposób bo tamtego nie zawsze da się użyć zapewne

3 maj 23:13
 Dany jest trójkąt ABC o polu równym 5,gdzie A=(5,3) B=(1,0).Prosta zawierająca wysokość
trójkąta ABC ma równanie y=2x−7.Wyznacz współrzędne punktu C.
D(x,2x−7)
Czyli wysokość opada z wierzchołka A,bo na leży do tej prostej.
No to licze:
|BD|2+|DA|2=|AB|2
(x−1)2+(2x−7)2+(5−x)2+(10−2x)2=25
x=3,x=5
D(3,−1),D=(5,3)−>odpada bo to współrzędne punktu A, S(4,1)
Czy do tego momentu nie ma błędu?Chciałem potem zapisać współrzędne punktu C w postaci takiej
jak punktu D poprzez wyznaczanie prostej prostopadlej do prostej y=2x−7 przechodzacej przez
punkt B i opisać okrąg na trójkącie ADC i skorzystać z faktu,że |SD|=|SC|
Dany jest trójkąt ABC o polu równym 5,gdzie A=(5,3) B=(1,0).Prosta zawierająca wysokość
trójkąta ABC ma równanie y=2x−7.Wyznacz współrzędne punktu C.
D(x,2x−7)
Czyli wysokość opada z wierzchołka A,bo na leży do tej prostej.
No to licze:
|BD|2+|DA|2=|AB|2
(x−1)2+(2x−7)2+(5−x)2+(10−2x)2=25
x=3,x=5
D(3,−1),D=(5,3)−>odpada bo to współrzędne punktu A, S(4,1)
Czy do tego momentu nie ma błędu?Chciałem potem zapisać współrzędne punktu C w postaci takiej
jak punktu D poprzez wyznaczanie prostej prostopadlej do prostej y=2x−7 przechodzacej przez
punkt B i opisać okrąg na trójkącie ADC i skorzystać z faktu,że |SD|=|SC|





 A=(5,3), B=(1,0)
1) k: y=2x−7 prosta zawierająca wysokość opuszczoną na bok BC
|AB|=5
A=(5,3), B=(1,0)
1) k: y=2x−7 prosta zawierająca wysokość opuszczoną na bok BC
|AB|=5

