t1
hiperwentylacja: opuszczanie modulu
x<0
Mam obliczyć minimum lokalne P(x)
Jak teraz to opuścić?
Wyszło mi, ze to co w środku zawsze jest mniejsze od zera, czyli opuszczam z minusem?
I wtedy wychodzi, że funkcja osiąga minimum dla 2
√2, a to jest niezgodne z dziedziną i jest
to niepoprawna odpowiedź
3 maj 14:47
3 maj 14:48
Jerzy:
Dlaczego x < 0 ?
3 maj 15:43
hiperwentylacja: Bo takie są warunki zadania, szukamy ujemnej współrzędnej odciętych punktu C, dla którego pole
trójkąta ABC jest jak najmniejsze
Wymienione w 1 poście P(x) to pole tego trójkąta jako połowa wartości bezwzględnej iloczynu
wektorów.
3 maj 15:53
Jerzy:
Zapisz człowieku treść zadania,a nie swoje wywody.
3 maj 16:10
ICSP: Widzę problemu z rozwiązywaniem równań ?
x2 − 12 = 0 ⇒ x = 2√3 v x = −2√3
Pierwszą odpowiedź odrzucasz ze względu na dziedzinę.
3 maj 16:14
hiperwentylacja: a co cie obchodzi tresc zadania, zadalem pytanie o jedna konkretna rzecz tresc zadania tu nie
ma nic do znaczenia
3 maj 16:14
hiperwentylacja: @ICSP no odrzucam ale co z monotonicznością funkcji? jesli odrzuce od tak jedno miejsce zerowe,
a ramiona funkcji są skierowane do góry to okaze sie, ze funkcja nie jest malejąca w żadnym z
przedzialow
3 maj 16:15
hiperwentylacja: myslalem ze wykres rysuje tak jakby moja dziedzina bylo R, a potem dopiero zaznaczam dziedzine
w ktorej rozpatruje monotonicznosc
3 maj 16:17
PW: Przede wszystkim
(x−6)(x−2) = x2−8x+12
Poza tym w mianowniku było x, a zrobiło się raptem x2.
3 maj 16:18
hiperwentylacja: @PW
To nie jest P(x) tylko P'(x) tak jak napisalem
3 maj 16:20
ICSP: No ale Ciebie nie interesuje to co się dzieje z funkcja dla x > 0
Rozważasz tylko x < 0.
Funkcja maleje, w punkcie x0 = −2√3 osiąga minimum a potem zaczyna rosnąć do
nieskończoności.
P.S.
Zgubiłeś minus w pochodnej.
3 maj 16:21
PW: Odnoszę się do pytania z 14:47. Widzę tam dwa błędy, a Ty swoje. Patrząc na Twój zapis z 16\:14
w ogóle żałuję, że się odezwałem.
3 maj 16:25
Jerzy:
Masz rację. Gó.no mnie obchodzi.
3 maj 16:28
hiperwentylacja:
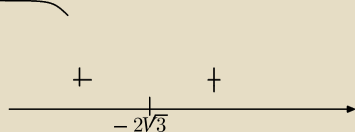
@ICSP no to tak by wygladala pochodna jezeli odrzucam z miejsca jedno miejsce zerowe niezgodne
z dziedzina
Czyli funkcja nie osiąga w ogóle minimum
3 maj 16:28
hiperwentylacja: @Jerzy no to skoro cię g*wno obchodzi to się nie wypowiadaj tutaj, może ktoś normalny pomoże
@16:28 coś ucięło, ale tam jest parabola z ramionami skierowanymi do góry
3 maj 16:31
ICSP: "Nie tak wygląda pochodną".
Masz problem z wykresem funkcji kwadratowej f(x) =x2 − 12.
3 maj 16:31
hiperwentylacja: No to nie mam innego pomysłu
Jak inaczej może wyglądać funkcja, która ma jedno miejsce zerowe i współczynnik a>0?
3 maj 16:35
ICSP: Ma dwa różne miejsca zerowe tylko jedno z nich Ciebie nie interesuje.
3 maj 16:37
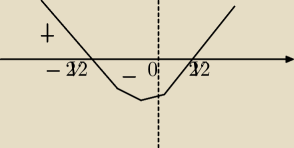
hiperwentylacja:
3 maj 16:44
ICSP: Na odwrót.
Przecież napisałem Ci, że zgubiłeś minus w pochodnej
Druga sprawa :
Funkcja w zerze nie jest ciągła. nie można w taki sposób rysować jej wykresu.
Dlatego rysujesz wykres tylko dal x < 0
3 maj 16:47
Jerzy:
Dla ciebie x2 − 12 zeruje się dla x = 2√2 lub −2√2.Gratuluję!
3 maj 16:49
hiperwentylacja: @ICSP
Gdzie zgubiłem minus?
| | −(x−6)(x−2) | |
x jest mniejsze od zera, a z postaci iloczynowej P(x) | |
| | wywnioskowałem ,że w |
| | x | |
takim wypadku całość funkcji wewnątrz modułu musi być ujemna
Dlatego opuściłem z minusem, czyli P'(x)={x
2−12}{x
2}
Źle?
3 maj 16:57
ICSP: No patrz, jednak funkcja pod modułem dla x < 0 przyjmuje wartości dodatnie.
3 maj 16:58
hiperwentylacja: aa dobra przepraszam, glupi blad i tyle zamieszania zrobil
calosc w module to będzie − podzielic na − czyli + −−>dodatnia
3 maj 17:01
hiperwentylacja:
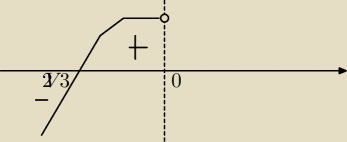
mam jeszcze pytanie − powinienem narysowac tak : ?
3 maj 17:04
ICSP: może być
3 maj 17:51
hiperwentylacja:
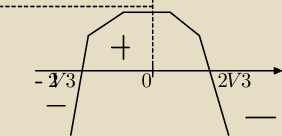
ok, dzieki za pomoc
a takie cos na maturze nie przejdzie? (wykres)
I napisanie : P'(x)>0⇔x∊(−2
√3,0), P'(x)<0⇔x∊(−
∞, −2
√3), P'(x)=0⇔x=−2
√3
A zatem funkcja P(x) rośnie w P'(x)>0. maleje w P'(x)<0 i uwzględniwszy dziedzinę P:x∊(−
∞,0),
osiąga najmniejszą wartość dla P(x
min)=P(−2
√3)?
3 maj 18:32
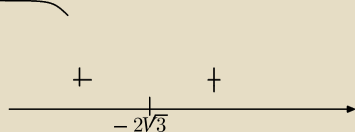 @ICSP no to tak by wygladala pochodna jezeli odrzucam z miejsca jedno miejsce zerowe niezgodne
z dziedzina
Czyli funkcja nie osiąga w ogóle minimum
@ICSP no to tak by wygladala pochodna jezeli odrzucam z miejsca jedno miejsce zerowe niezgodne
z dziedzina
Czyli funkcja nie osiąga w ogóle minimum

 mam jeszcze pytanie − powinienem narysowac tak : ?
mam jeszcze pytanie − powinienem narysowac tak : ?
 ok, dzieki za pomoc
a takie cos na maturze nie przejdzie? (wykres)
I napisanie : P'(x)>0⇔x∊(−2√3,0), P'(x)<0⇔x∊(−∞, −2√3), P'(x)=0⇔x=−2√3
A zatem funkcja P(x) rośnie w P'(x)>0. maleje w P'(x)<0 i uwzględniwszy dziedzinę P:x∊(−∞,0),
osiąga najmniejszą wartość dla P(xmin)=P(−2√3)?
ok, dzieki za pomoc
a takie cos na maturze nie przejdzie? (wykres)
I napisanie : P'(x)>0⇔x∊(−2√3,0), P'(x)<0⇔x∊(−∞, −2√3), P'(x)=0⇔x=−2√3
A zatem funkcja P(x) rośnie w P'(x)>0. maleje w P'(x)<0 i uwzględniwszy dziedzinę P:x∊(−∞,0),
osiąga najmniejszą wartość dla P(xmin)=P(−2√3)?