Trojkat pikus: MATURA W trójkącie równoramiennym suma długości ramienia i promienia okręgu opisanego na tym trójkącie równa jest m a wysokość trójkąta równa jest 2. a)Wyznaczyć długość ramienia jako funkcję parametru m oraz wartość m , dla której kąt przy wierzchołku trójkąta równy jest 120^o ? b)Dla jakich wartości m zadanie ma rozwiązanie?

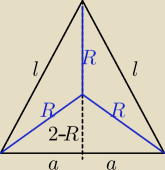
iteRacj@: l − długość ramienia trójkąta, l>0, R>0, m>0 l+R=m h=2 z tw.Pitagorasa R²=(2−R)²+a² z tw.Pitagorasa l²=2²+a² ⇒ a²=l²−4 R²=(2−R)²+l²−4 l²−4R=0 R=m−l l²−4l−4m=0 Δ=16−4(−4m)=16(m+1)≥0, m≥−1

	4+4√m+1
l1=
	2

	4−4√m+1
l2=		, dodaję warunek: 4−4√m+1≥0 ⇒ 1−≤m≤0 nie spełnia warunków zadania
	2

Wyznaczam długość ramienia trójkąta jako funkcję parametru m:

	4+4√m+1
l=
	2

pikus: Czyli odpowiedź na podpunkt b to m>0

iteRacj@: Nie, bo gdyby np. m=1 to jak wysokość Δ mogłaby mieć 2 ?

pikus: No to jakie to m powinno być bo nie wiem

pikus: Czy m>2 bo ta suma promieni ma być od 2 większą czy równa?

iteRacj@: Zauważyłam zamieniony minus z plusem w obliczeniach, poprawiam. l²−4R=0 i R=m−l ⇒ l²+4l−4m=0

	−4+4√m+1
Stąd l=		=2√m+1−2
	2

iteRacj@: 10:38 Suma długości ramienia i promienia okręgu opisanego na tym trójkącie musi być większa od wysokości czyli m>2. Ale mamy również mocniejszy warunek: skoro wysokość tego trójkąta równoramiennego opuszczona na podstawę ma długość 2, to samo ramię też musi być od niej dłuższe. l>2 l=2√m+1−2>2 spełnione dla każdego m>3 Jednoczesnie promień okręgu opisanego na tym trójkącie musi być krótszy niż wysokość. 0<R<2, R=m−l 0<m−l<2 0<m−(2√m+1−2)<2 0<m−2√m+1+2<2 0<(m+1)−2√m+1+1<2 0<(√m+1)²−2√m+1+1<2 1/ (√m+1)²−2√m+1+1>0 spełnione dla każdego m≥−1 2/ (√m+1)²−2√m+1−1<0 spełnione dla m<2+2√2 Czy ktoś ma cierpliwość sprawdzić, czy dobrze to policzyłam?