tr kundermann: Oblicz cos kąta zawartego między wysokosciami dwoch sasiednich scian bocznych ostroslupczysyna prawidlowego czworokatnego, w ktorym wszystkie krawedzie sa tej samej dlugosci

kundermann: Wyszlo mi −1/3 a w odp jest 2/3

Bleee: To pokaż swoje obliczenia

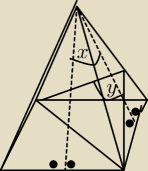
kundermann: ja policzyłem kąt y, kolega kąt x. koledze kurasikowi wyszło dobrze, a mi zle

Bleee: PS. Na chłopski rozum − wyszedł ci cosx<0 czyli kat jest większy od 90^o podczas gdy kat u podstawie wynosi 90^o, czy jest to możliwe?

Bleee: Faktycznie... Cosinus tego kąta będzie ujemny.

kundermann: cos (y/2) wyszedl mi a/2 / a√3/2 czyli 1/√3 potem ze wzoru na cos podwojoinego kąta cos y=−1/3

kundermann: @Bleee ale o ktory z zaznaczonych kątow wedlug ciebie chodzilo autorom zadania? bo ten i ten kąt jest kątem zawartym między dwiema wysokosciami

Bleee: Szczerze... Robilbym ten kat co Ty

kundermann: czyli 2 wyniki i oba poprawne?

Bleee: Jak dla mnie to oba poprawne

Wolodyjowski: Jak dla mnie poprawna jest wersja z cos ruwny 2/3 napisaliby wszak ze wysokosc ma wychodzic z woerzcholczysyna u podstawy

Bleee: Wołodyjowski... A niby dlaczego w przypadku ściany bocznej trójkąt ma mieć tylko jedna wysokość? Pozostałe dwie w magiczny sposób znikają?

Mila:

	1		a√2
|EF|=		AC|=
	2		2

	a√3
h=
	2

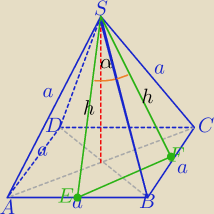
W ΔEFS: |EF|²=h²+h²−2*h*h *cos α⇔|EF|²=2h²*(1−cosα)

	a√2		a√3
(		)2=2*(		)2*(1−cosα)
	2		2

a2		a2*3		2
	=2*		*(1−cosα) / *
2		4		3a2

1
	=1−cosα
3

	2
cosα=
	3

========