ostrosłup Michał: Podstawą ostrosłupa ABCDS jest prostokąt ABCD , w którym |AB | = 1, |BC | = √2 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

Maciess: https://www.zadania.info/d501/2343339

Michał: No tak, tylko to rozwiązanie do mnie nie trafia. Nie rozumiem czemu na podstawie BC wybierali jakiś punkt G

Michał: nie można było tego rozpatrywać z trójkąta BDF?

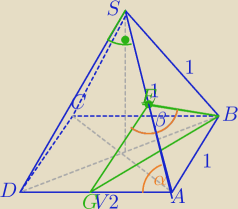
Mila: 1) ΔABS− Δrównoboczny ΔADS−Δrównoramienny prostokątny,| ∡DSA|=90^o 2) BE⊥AS,

	√3
|EB|=		− Spodek wysokości ΔABS leży w środku AS
	2

DS musimy odpowiednio przesunąć równolegle GE||DS i GE⊥AS |∡DAS|=45^o

	1
|GE|=|AE|=
	2

	1
|GA|=		√2
	2

3) licz dalej sam GB i tw. cosinusów

Maciess: To nie byłby wtedy kąt między ścianami. Wszystko masz tam ładnie opisane. Oba te odcinki musza być prostopadłe do krawędzi bocznej

Mila: Kąt dwuścienny. Kątem liniowym kąta dwuściennego nazywa się kąt płaski będący częścią wspólną tego kąta dwuściennego oraz płaszczyzny prostopadłej do jego krawędzi. Krawędź szukanego kąta to SA. Płaszczyzna GEB jest prostopadła do tej krawędzi. Spodek wysokości BE znajduje się w środku SA, spodek DS jest w innym miejscu, musimy zastosować przesunięcie. Jeżeli ciąłbyś nożem takie ciastko zaczynając od punktu B i prostopadle do krawędzi AS to właśnie będzie jak na rysunku.

Michał: Dzięki Mila, już rozumiem

Michał: i mam nadzieję że na maturze takie się nie pojawi

Godzio: Mam wrażenie, że na ostatnich maturach, kąt dwuścienny został zastąpiony zadaniem optymalizacyjnym wykorzystującym pochodną.

Mila: Dobranoc