Wyznacz wartości parametru paweu: Wyznacz wartosci parametru k dla ktorych równanie x³−9x=k ma dwa rozwiązania w przedziale <0;3>

ICSP: f(x) = x³ − 9x − k Wystarczy aby: f(0) ≥ 0 f(3) ≥ 0 f(√3) < 0

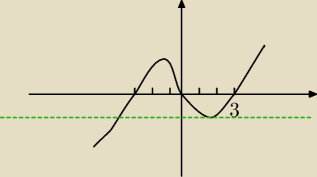
Godzio: Albo tak: f(x) = x³ − 9x = x(x − 3)(x + 3) f'(x) = 3x² − 9 = 3(x − √3)(x + √3) x = √3 − minimum lokalne równe f(√3) = 3√3 − 9√3 = − 6√3 x = −√3 − maksimum lokalne równe f(−√3) = 6√3 Po wykresie wnioskujemy, że istnieją dwa rozwiązania w przedziale <0,3>, gdy k = − 6√3

paweu: Nie do końca rozumiem. W odpowiedziach jest k∊(−6√3;0>

paweu: Ok, rozumiem, dzięki!

Godzio: Ano tak źle zrozumiałem polecenie, dwa rozwiązania w przedziale <0,3>, a poza tym może być gdziekolwiek, więc odpowiedź to (−6√3,0>