Jak wyznaczyć współrzędne punktu B? kapiszon: Dane sa punkty a (−4,1) c (2,−1) lezace na okregu o srodku w punkcie s i promieniu dlugosci r. Środek tego okręgu ma obie współrzędne ujemne i jest oddalony o √13 od prostej l o rownaniu y=−3/2x+1/2. Wyznacz równanie tego okręgu oraz współrzędne takiego punktu B leżącego na tym okręgu, że trójkąt ABC jest prostokątny. Wie ktoś jak wyznaczyć ten punkt B, bo na tym się zatrzymałem.

kapiszon: Czy to wystarczy obliczyć z wzoru na odcinek o koncach w punktach A,B i C,B, kiedy znamy długość tego odcinka bo sa to 2 promienie tego koła, ponieważ przeciwprostokątna trójkąta wpisanego w okrąg jest zawsze średnicą?

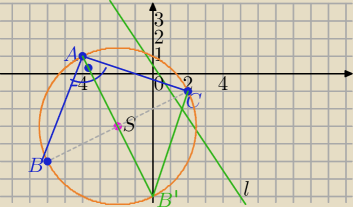
Mila: A= (−4,1) ,C= (2,−1) 1) l: y=−3/2x+1/2⇔3x+2y−1=0 S=(a,b) −środek okręgu, a<0 i b<0 2) Środek okręgu leży na symetralnej cięciwy AC s: (x+4)²+(y−1)²=(x−2)²+(y+1)² stąd: s: y=3x+3− równanie symetralnej AC S=(a, 3a+3) 3) d(S,l)=√13⇔

|3a+2(3a+3)−1|
	=√13⇔
√32+22

|9a+5|=13 9a+5=13 lub 9a +5=−13 9a=8 lub 9a=−18

	8
a=		>0 lub a=−2
	9

S=(−2, −3) 4)r=|AS|=√(−2+4)²+(−3−1)²=√20 r=2√5 (x+2)²+(y+3)²=20 równanie okręgu 5) ΔABC jest prostokątny⇔Kąt A lub kąt C jest kątem wpisanym w okrąg opartym na średnicy Wektorowo najprościej AS→=[2, −4] S=(−2,−3)→T_[2,−4]⇒B'=(−2+2,−3−4)=(0,−7) CS^→=[−4,−2] S=(−2,−3)→T_[−4,−2]⇒B=(−2−4,−3−2)=(−6,−5)

kapiszon: Dziękuję ślicznie.

Mila: