Pola
Lmao: Cześć, mógłby mnie ktoś nakierować jakim sposobem należy wykonać te zadania:
1. Najdłuższy bok trójkąta rozwartokątnego ma długość 60 a wysokości poprowadzone z obu jego
końców mają długości 12 i 20. Oblicz pole
2. Na ostrokątnym trójkącie równoramiennym opisano okrąg. Odległość środka tego okręgu od
podstawy i ramienia są równe odpowiednio 3 i √5. Oblicz pole
1 maj 13:35
iteRacj@:
2/
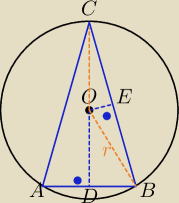
|CO|=|OB|=r
|CD|=r+
√5
|OE|=
√5, |OD|=3
skorzystaj z tw. Pitagorasa w ΔCOE, ΔDOB
i z podobieństwa ΔCOE∼ΔCDB (kkk)
1 maj 15:58
Godzio:
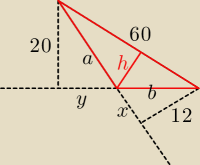
Dość prymitywny sposób, ale nie wymyśliłem nic lepszego ..
| 12 * a | | 20 * b | | 5 | |
| = |
| ⇒ 6a = 10b ⇒ a = |
| b |
| 2 | | 2 | | 3 | |
20
2 + y
2 = a
2
(b + y)
2 + 20
2 = 60
2
| | 25 | |
400 + y2 = |
| b2 ⇒ 3600 + 9y2 = 25b2 |
| | 9 | |
(b + y)
2 + 20
2 = 60
2 ⇒ (b + y)
2 = 40 * 80 ⇒ b + y = 40
√2 ⇒ y = 40
√2 − b
3600 + 9(3200 − 80
√2b + b
2) = 25b
2
16b
2 + 720
√2b − 32400 = 0
b
2 + 45
√2b − 2025 = 0
Δ = 4050 + 8100 = 12150
√Δ = 45
√6
| | −45√2 + 45√6 | | 45√2(√3 − 1) | |
b1 = |
| = |
| |
| | 2 | | 2 | |
b
2 < 0
P = 10b = 225
√2(
√3 − 1)
1 maj 16:06
Lmao: Dzięki wielkie za pomoc
1 maj 16:44
Maciess:
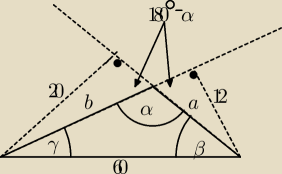
Dorzuce swoje rozwiązanie 1szego
Z trojkątów podobnych (KKK)
Alfa jest kątem rozwartym więc pozostałe są ostre
| | 20 | | 1 | | 2√2 | |
sinβ= |
| = |
| ⇒ cosβ= |
| |
| | 60 | | 3 | | 3 | |
Tw. cosinusow dla kąta β
| | 3 | | 3 | | 2√2 | |
b2=602+( |
| b)2−2*60* |
| b* |
| |
| | 5 | | 5 | | 3 | |
P=1/2*60*b*sinγ= 225
√2(
√3 − 1)
1 maj 17:34
 2/
|CO|=|OB|=r
|CD|=r+√5
|OE|=√5, |OD|=3
skorzystaj z tw. Pitagorasa w ΔCOE, ΔDOB
i z podobieństwa ΔCOE∼ΔCDB (kkk)
2/
|CO|=|OB|=r
|CD|=r+√5
|OE|=√5, |OD|=3
skorzystaj z tw. Pitagorasa w ΔCOE, ΔDOB
i z podobieństwa ΔCOE∼ΔCDB (kkk)
 Dość prymitywny sposób, ale nie wymyśliłem nic lepszego ..
Dość prymitywny sposób, ale nie wymyśliłem nic lepszego ..
 Dorzuce swoje rozwiązanie 1szego
Z trojkątów podobnych (KKK)
Dorzuce swoje rozwiązanie 1szego
Z trojkątów podobnych (KKK)