ty debil: Czy istnieje czworokąt, którego pole jest równe polu dwóch trójkątów prostokątnych i nie jest to prostokąt?

debil: już nieważne − jest, np. deltoid wpisywalny w okrąg

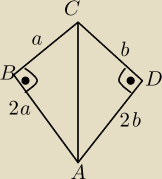
debil: jak zatem wykazac, ze np taka figura nie jest deltoidem, a prostokątem, wiedząc, że jej pole jest równe a²+b²? Mam wykazać, że a=2b? jak to zrobić? Bo wydaje mi się, że najtrudniejsze już zrobiłem − Pabcd=Pabc+Padc=a²+b² Korzystam ze wzoru : 1/2*AB*CB*sinabc Tak samo w Padc I wychodzi : a²(sinabc−1)+b²(sinadc−1)=0 Zatem zarówno kąt abc jak i kąt adc jest kątem prostym, czyli czworokąt składa się z dwóch trójkątów prostokątnych No ale jak teraz wykazać, że to nie np. deltoid, a konkretnie prostokąt? a=2b

Maciess: Długości przekątnych. Czy to oryginalna treść zadania? Przypomina zadanie z próbnej nowej ery

iteRacj@: Czy istnieje czworokąt, którego pole jest równe polu dwóch trójkątów prostokątnych i nie jest to prostokąt? Pole każdego czworokąta, możesz zapisać jako sumę pól dwóch trójkątów prostokątnych.

debil: @iteRacj@ takich, ktore zawieraja sie w jego powierzchni? nie wydaje mi sie @Maciess tak, z probnej ery

Maciess: To chyba źle oznaczyłes. Zaraz odgrzebie te maturę.

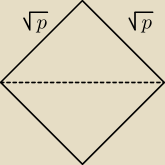
iteRacj@: Niech pole czworokąta niebędącego prostokątem wynosi p cm². Jest ono równe polu kwadratu o boku √p cm (taki jest na rysunku). Pole tego kwadratu jest sumą pól dwóch trójkątów prostokatnych.

debil: ale przeciez dokladnie to samo napisalem w poscie z deltoidem − nie jest prostokatem a mimo to spelnia warunki zadania @Maciess jak dowiesc tego, ze przekatne sa rownej dlugosci?

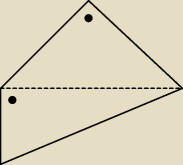
iteRacj@: Wpis z 11:44 zmienia warunki zadania. I wtedy nie dla każdego czworokąta jest to prawda. Ale nadal wiemy, że takie czworokąty istnieją.

Maciess: Długosci boków czworokąta wypukłego ABCD wynoszą |AB|=a |BC|=2a |CD|=b |AD|=2b Wykaż, że jesli pole czworokąta ABCD jest równe a²+b², to jest on prostokątem. Czy mowa o tym zadaniu?

debil: tak

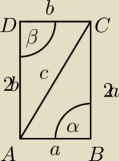
Maciess: P=1/2*2a²sinα+1/2*2b²sinβ a²sinα+b²sinβ=a²+b² ⇔ sin α=1 ∧ sinβ=1 ⇔ α=90^o ∧ β=90^o Czyli dwa prostokątne c²=5a² c²=5b² 5a²=5b² a=b Oczywiście cos dopisać i gotowe

debil: proscizna.... dzieki

PW: Okrąg, średnica. Każdy kąt wpisany oparty na średnicy to kąt prosty. Dwa wierzchołki po różnych stronach średnicy − dwa trójkąty prostokątne − czworokąt. Takich czworokątów jest nieskończenie wiele (nie muszą to być prostokąty ani deltoidy).