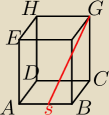
 Kwadrat ABCD jest podstawą graniastosłupa ABCDEFGH. Odcinek łączący środek S krawędzi podstawy
AB z wierzchołkiem G ma długość d, a prosta SG jest nachylona do płaszczyzny DCGH pod kątem o
mierze α. Wyznacz pole powierzchni bocznej prostopadłościanu.
jak narysować ten kąt α? bo nie rozumiem jak go nachylić do tej płaszczyzny? + z odpowiedzi
wychodzi że sinα*d=krawędź podstawy i to też mi nie pasuje
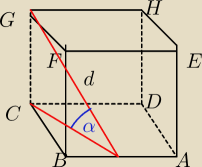
Kwadrat ABCD jest podstawą graniastosłupa ABCDEFGH. Odcinek łączący środek S krawędzi podstawy
AB z wierzchołkiem G ma długość d, a prosta SG jest nachylona do płaszczyzny DCGH pod kątem o
mierze α. Wyznacz pole powierzchni bocznej prostopadłościanu.
jak narysować ten kąt α? bo nie rozumiem jak go nachylić do tej płaszczyzny? + z odpowiedzi
wychodzi że sinα*d=krawędź podstawy i to też mi nie pasuje 
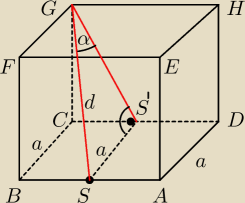
| a | |
=sinα ⇒ a=d*sinα | |
| d |
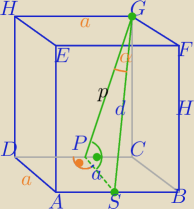 1) rysujemy rzut prostopadły odcinka SG na płaszczyznę DCGH
Rzutem punktu S jest punkt P,
rzutem punktu G jest G
∡SGP=α
2)ΔSPG− Δprostokątny,
1) rysujemy rzut prostopadły odcinka SG na płaszczyznę DCGH
Rzutem punktu S jest punkt P,
rzutem punktu G jest G
∡SGP=α
2)ΔSPG− Δprostokątny,
| a | ||
sinα= | ||
| d |
| p | ||
cosα= | ||
| d |
| 1 | ||
H2+( | a)2=p2 | |
| 2 |
| 1 | ||
H2=d2*cos2α− | *d2*sin2α | |
| 4 |
| 1 | 4−5sin2α | |||
H2=d2*(cos2α− | sin2α)=d2*( | ) | ||
| 4 | 4 |
| d√4−5sin2α | ||
H= | ||
| 2 |
| d√4−5sin2α | ||
Pb=4*a*H=4*d sinα* | ||
| 2 |


