Całka iterowana Azmuth: Zmień kolejność całkowania w całce iterowanej: ∫₋₁¹dx ∫₀^|x| f(x,y) dy Czy odpowiedź ∫₀¹dy ∫_−y^y f(x,y) dy jest poprawna ?

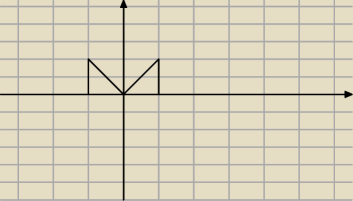
mat: x ∊<−1,1>, y∊(0,|x|) taki masz zakres całkowania

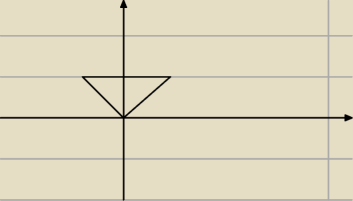
mat: y∊<0,|x|>** y∊<0,1>, x∊<−y,y> oznaczałby cos takiego

Azmuth: To jak mam to zrobić ?

Azmuth: −y≥x≥y Wtedy wezmę te części leżące niżej

mat: nie, bo przecież y≥0, wiec −y≥y ma jedynie rozwiazanie y=0

Azmuth: Nie rozumiem, przecież jeżeli narysuję sobie prostą x=y, to następnie żeby dostać prawą część mojego obszaru potrzebuję nierówności x ≥ y, czyli ten prawy trójkąt. I analogicznie sytuacja dla drugiej, lewej strony... Chyba, że źle myślę, wtedy proszę o wytłumaczenie

mat: niech y=0.5 Jakie x'kys spełniają −0.5≥x≥0.5 ?

mat: Najłatwiej by było napisać ∫₀¹dy∫₋₁¹f(x,y)dx − ∫₀¹dy∫_−y^yf(x,y)dx

Azmuth: No żadne nie spełniają, myślałem w kategoriach prostych i przeoczyłem proste obliczenie W każdym razie, dlaczego tak jest najłatwiej, nie rozumiem tego, nie da się zapisać w postaci jednej całki ?

Azmuth: Czy zapis ∫₀¹ dy ∫₀^y f(x,y)dx + ∫₀¹ dy ∫_−y⁰ f(x,y)dx ma tutaj sens ?

mat: Właśnie wydaje się że nie, ale może nie widzę teraz, no od prostokąta odejmuję twój trójkąt

mat: No ma sens ale to dalej nie to

Azmuth: Bo zobacz, pierwszy składnik sumy to ten prawy prostokąt a drugi to lewy. Zresztą, okaże się dzisiaj na ćwiczonkach Bardzo Ci dziękuję za pomoc i trafne uwagi !

mat: No niestety nie, to dalej obie części tego trójkąta,, nad ". Powodzenia