Wartość bezwzględna.
Lejla: Liczba ujemnych rozwiązanie równania I−(x+1)²+4I =5−IxI jest równa
A=0
B=2
C=3
D=4
29 kwi 20:27
Eta:
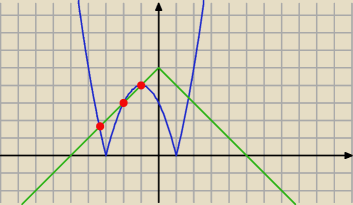
Odp: C
29 kwi 21:06
PW: Bez "maszyny do rysowania wykresów":
Lewa strona równania jest liczbą nieujemną dla dowolnej x, tak więc rozwiązania mogą istnieć
tylko gdy
5 − |x| ≥ 0,
to znaczy gdy
|x| ≤ 5
−5 ≤ x ≤ 5.
Interesują nas rozwiązania ujemne, bierzemy więc pod uwagę
−5 ≤ x < 0.
Dla takich x równanie ma postać
|−(x+1)
2+4| = 5+x
i jest równoważne alternatywie dwóch równań:
−(x+1)
2 + 4 = 5+x lub −(x+1)
2 + 4 = −(5+x)
−x
2−2x−1+4 = 5+x lub −x
2−2x−1+4 = −5 − x
−x
2−3x−2 = 0 lub −x
2−x+8 = 0
x
2+3x+2 = 0 lub x
2+x−8 = 0
Pierwsze z tych równań ma rozwiązania −1 oraz −2 (oba należą do przedziału <−5, 0), zaś drugie
| | −1−√33 | | −1+√33 | |
|
| oraz |
| .(tylko pierwsze z nich należy do przedziału <−5, 0). |
| | 2 | | 2 | |
Odpowiedź: Badane równanie ma trzy rozwiązania ujemne.
29 kwi 22:48
Eta:
Czas na maturze ..."droższy od pieniędzy"

29 kwi 22:50
Eta:
A szczególnie w zadaniach testowych

29 kwi 22:52
PW: Rzekłaś, o Pani.
Przy okazji dziękuję (wiesz za co).
29 kwi 22:59
Eta:


29 kwi 23:02
Lejla: @PW jestes wielki❤
30 kwi 20:21
Eta: 
30 kwi 20:29
Eta:
No i masz "babo placek"

30 kwi 20:31
Lejla: Ahhahahahha, zazdrosna? 😆😘
30 kwi 20:36
PW: Chciała poznać metodę "czysto algebraiczną", bez rysowania wykresów

Nie wzięła pod uwagę, że trochę żartowałem (zadanie testowe nie wymaga uzasadnień, a pytanie
"ile" nie wymaga wyliczania tych rozwiązań).
30 kwi 20:41
Lejla: No ale wiesz to rozwlekłe rozwiazanie bylo bardziej dla mnie niz dla egzaminatora na maturze

30 kwi 20:43
 Odp: C
Odp: C






 Nie wzięła pod uwagę, że trochę żartowałem (zadanie testowe nie wymaga uzasadnień, a pytanie
"ile" nie wymaga wyliczania tych rozwiązań).
Nie wzięła pod uwagę, że trochę żartowałem (zadanie testowe nie wymaga uzasadnień, a pytanie
"ile" nie wymaga wyliczania tych rozwiązań).
