Sześcian przecięto płaszczyznami Dwite: Sześcian ABCDA'B'C'D' przecięto płaszczyznami AB'D' i CB'D'. Oblicz cosinus kąta między tymi płaszczyznami. Mógłby mi ktoś to wytłumaczyć?

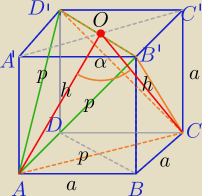
Mila: 1) ΔAB'D', ΔCB'D'− Δrównoboczne o boku p=a√2 AO⊥B'D', CO⊥B'D'

	a√2*√3		a√6
h=		=
	2		2

2) W ΔACO: |AC|²=h²+h²−2*h*h*cosα

	a√6
(a√2)2=2*(		)2*(1−cosα)
	2

	6a2
2a2=2*		*(1−cosα)
	4

2=3*(1−cosα)

2
	=1−cosα
3

	1
cosα=
	3

==========

Dwite: Dziękuję