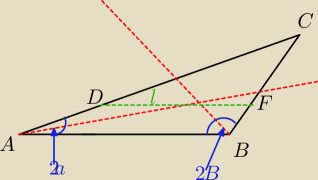
planimetria salv: W trojkacie ABC poprowadzono dwusieczne katow A i B a następnie przez punkt ich przecięcia − prostą l równoległą do boku AB.Prosta l przecina bok AC w punkcie D,a bok BC w punkcie F.Udowodnij,że |DF|=|AD|+|BF| ΔABC~ΔDFC (kkk) i pewnie cos kombinowac z talesem ale mi nie wychodzi

wredulus_pospolitus: Niech P to punkt przecięcia się tych dwusiecznych zauważ, że ΔBPF oraz Δ APD to trojkaty równoramienne

wredulus_pospolitus: Wnioskowanie: 1) ∡PDC = 2α 2) więc ∡PDA = 180 − 2α 3) więc ∡DPA = 180 − (180 − 2α) − α = α więc |AD| = |DP| analogicznie drugi trójkąt

salv: dziekuje