Geometria, konkurs. bongocat: Ramiona trapezu ABCD o podstawach |AB|=10 i |CD|=4, przedłużono do przecięcia się w punkcie F. Przez środek E odcinka DC poprowadzono prostą AE, która przecięła prostą BF w punkcie G, podobnie prosta BE przecina prostą AF w punkcie H. Wykaż, że HG | | AB. Oblicz długość odcinka HG.

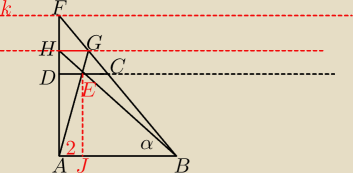
an: Zauważ , jeżeli wierzchołek F trójkąta ABF będziemy przesuwać po prostej k równoległej do AB to powstające trójkąty będą miały takie same podstawy i wysokości czyli DC=D'C' i HG=H'G' czyli obojętnie jaki trójkąt o podstawie AB i wierzchołku F leżącym na prostej k będziemy rozpatrywać. Z podobieństw trójkątów na p/w rysunku HG=2.5

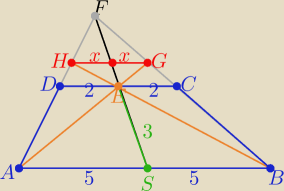
Eta: 1 / FE i FS −− długości środkowych w trójkątach DCF i ABF i z podobieństwa trójkątów ...... HG II AB 2/ (*) W każdym trapezie odcinek łączący ramiona i przechodzący przez punkt przecięcia przekątnych ma długość średniej harmonicznej długości podstaw

	a−b
dodatkowo zaznaczyłam : |ES|=		−−− dł. odcinka łączącego środki podstaw
	2

z 1/ czworokąt ABGH jest też trapezem to w trapezie ABGH z (*) :

	2|AB|*|HG|
|DC|=		−−− średnia harmoniczna podstaw AB i HG
	|AB|+|HG|

	20*2x
4=
	10+2x

2x=|HG|= ................

Eta: Troszkę się spóźniłam

bongocat: Dzięki, ale ten wzór na odcinek łączący środki podstaw chyba nie jest poprawny, bo przecież możemy dowolnie wydłużać trapez w taki sposób, że długości podstaw się nie zmienią a ten odcinek już tak

bongocat: I dalej nie rozumiem, z podobieństwa których trójkątów wynika, że HG || AB?

Eta: Słuszna uwaga sorry

	a−b
|ES|=		tylko wtedy gdy przedłużenia ramion przecinają się pod kątem prostym
	2

czyli suma miar kątów przy dłuższej podstawie jest równa 90^o