okregi
Michał: Wyznacz równanie okręgu o środku w punkcie S=(3,3) do którego jest styczny wewnętrznie okrąg o
równaniu (x−2)2 + (y−1)2 = 5
Zrobiłem to tak że odległośc środków tych okręgów równa jest różnicy długości promieni czyli
|SS1| = |r1 − r2|
√5 = |√5 − r2|
czyli r2 = 2√5
i równanie okręgu (x−3)2 + (y−3)2 = 20
mogę tak robić takie zadanie? pytam bo robię sobię maturkę i jest to zadanie za 5pkt a w
odpowiedziach wyznaczają równanie prostej przechodzącej przez środki tych okręgów i
współrzędne punktu styczności.
28 kwi 16:37
Basia: oczywiście, jest ok

Twoje rozwiązanie jest lepsze.
28 kwi 17:03
Michał: ta ilośc punktów mnie wprowadziła w błąd

dziękuję
28 kwi 17:09
Mila:
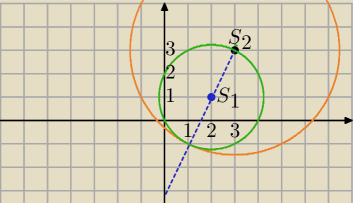
O
1: (x−2)
2 + (y−1)
2 = 5 , r
1=
√5
S
2=(3,3) ∊O
1
R
2=2r
1=2
√5
(x−3)
2+(y−3)
2=(2
√5)
2
28 kwi 19:11
 Twoje rozwiązanie jest lepsze.
Twoje rozwiązanie jest lepsze.
 dziękuję
dziękuję
 O1: (x−2)2 + (y−1)2 = 5 , r1=√5
S2=(3,3) ∊O1
R2=2r1=2√5
(x−3)2+(y−3)2=(2√5)2
O1: (x−2)2 + (y−1)2 = 5 , r1=√5
S2=(3,3) ∊O1
R2=2r1=2√5
(x−3)2+(y−3)2=(2√5)2