Zbadaj wzajemne położenie prostej i okręgów o równaniach Andrzej1234: Proszę o sprawdzenie mojego rozwiązania w ostatnim zadaniu,które chce dzisiaj zrozumieć: Zbadaj wzajemne położenie prostej i okręgów o równaniach o : (x+1)²+(y−3)²=9 l y=2 postanowiłem to rozwiazązać za pomocą ukladu równań (x+1)²+(y−3)²=9 y=2 (x+1)²+(2−3)²=9 y=2 x²+2x+1+2=9 y=2 x²+2x=6 y=2 I dalej nie wiem co robić,jak to ruszyć?

jc: Okrąg zaczyna się na wysokości 3−3=0, a kończy na wysokości 3+3=6. Prosta pozioma na wysokości 2 przecina okrąg w 2 punktach.

Andrzej1234: Własnie się zorientowałem,że raczej tego się tak nie da zrobic, ma ktoś jakieś pomysły?

Andrzej1234: Jc jak to obliczyłeś?

6latek: Inaczej . Policz odlelosc srodka okregu od prostej y=2 (czyli odleglosc d ) potem d=r 1 punkt stycznoosci d>r −nie ma punktow stycznoscoi d<r −dwa punkty przeciecia

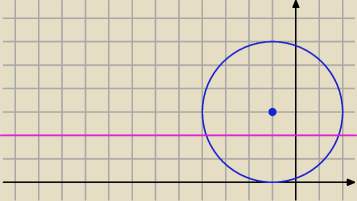
Maciess: W takim przypadku chyba lepiej sobie to narysowac

Andrzej1234: Tutaj z równania okręgu wynika ,ze promień ma 3 wiec jest większy od odległości czyli d i dlatego ma dwa punkty przecięcia o to chodzi?

Maciess: W zadaniach gdzie współrzędne są punktami kratowymi moge chyba opierać swoje wnioski na rysunkach, prawda?

6latek: Dlaczego nie policzyles d ? masz wzor na odleglosc punktu od prostej

Mila: o : (x+1)²+(y−3)²=9 l : y=2 1) Algebraicznie (x+1)²+(2−3)²=9 (x+1)²=8 (x+1)=√8 lub x+1=−√8 x=−1+2√2 lub x=−1−2√2 Dwa punkty wspólne A=(−1+2√2,2) , B=(−1−2√2,2) Jeżeli to jest test wyboru, to rysuj i patrz na rysunek.