Zbadaj wzajemne położenie dwóch okręgów o równaniach
Andrzej1234: Dzień dobry
Proszę o pomoc w rozwiązaniu zadania :
Zbadaj wzajemne położenie dwóch okręgów o równaniach
o1: (x−1)2+y2= 16, o2:x2+y2+4x−8y+19=0
27 kwi 18:50
PW: Obliczyć odległość środków tych okręgów i porównać ją z sumą oraz z różnicą promieni.
27 kwi 19:03
Andrzej1234: W takim wypadku
w o1
środek to (1,0) a promień to 16 z kolei o2 środek to (2,√8 ) z kolei promień to −19?
27 kwi 19:21
PW: Oj, kwadrat promienia to 16.
o2:
(x2+4x+4) − 4 + (y2−8y+16) − 16 + 19 = 0
(x+2)2 + (y−4)4 = 1
27 kwi 19:38
Mila:
O
1: (x−1)
2+y
2= 16, O
2:x
2+y
2+4x−8y+19=0⇔
O
1: (x−1)
2+y
2=4
2 , S
1=(1,0), R=4
O
2: (x
2+4x+4) +(y
2−8y+16)−4−16+19=0
O
2: (x+2)
2+(y−4)
2=1, S
2=(−2,4), r=1
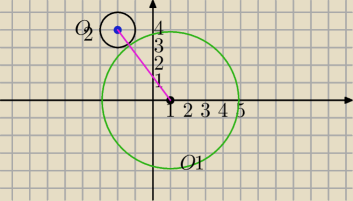
Możesz narysować i zobaczyć ( nie zawsze jest to dokładne)
albo
Możesz rozwiązać układ równań
albo
Wykonać prosty rachunek:
R+r=4+1=5
|S
1S
2|=
√(−2−1)2+(4−0)2=
√9+16=5
Okręgi są styczne zewnętrznie− mają jeden punkt wspólny.
https://www.matmana6.pl/wzajemne-polozenie-dwoch-okregow
27 kwi 23:34
 O1: (x−1)2+y2= 16, O2:x2+y2+4x−8y+19=0⇔
O1: (x−1)2+y2=42 , S1=(1,0), R=4
O2: (x2+4x+4) +(y2−8y+16)−4−16+19=0
O2: (x+2)2+(y−4)2=1, S2=(−2,4), r=1
Możesz narysować i zobaczyć ( nie zawsze jest to dokładne)
albo
Możesz rozwiązać układ równań
albo
Wykonać prosty rachunek:
R+r=4+1=5
|S1S2|=√(−2−1)2+(4−0)2=√9+16=5
Okręgi są styczne zewnętrznie− mają jeden punkt wspólny.
https://www.matmana6.pl/wzajemne-polozenie-dwoch-okregow
O1: (x−1)2+y2= 16, O2:x2+y2+4x−8y+19=0⇔
O1: (x−1)2+y2=42 , S1=(1,0), R=4
O2: (x2+4x+4) +(y2−8y+16)−4−16+19=0
O2: (x+2)2+(y−4)2=1, S2=(−2,4), r=1
Możesz narysować i zobaczyć ( nie zawsze jest to dokładne)
albo
Możesz rozwiązać układ równań
albo
Wykonać prosty rachunek:
R+r=4+1=5
|S1S2|=√(−2−1)2+(4−0)2=√9+16=5
Okręgi są styczne zewnętrznie− mają jeden punkt wspólny.
https://www.matmana6.pl/wzajemne-polozenie-dwoch-okregow