Obraz odcinka AB w jednokładności
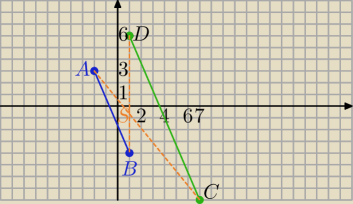
xD: Obrazem odcina AB, gdzie A = (−2, 3), B = (1, −4) w jednokładności o środku S i skali k < 0
jest odcinek CD, w którym C = (7, −8), D = (1, 6). Wyznacz środek i skalę tej jednokładności.
Proszę o pomoc nie wiem jak zrobić to zadanko.
26 kwi 22:10
Mila:
C = (7, −8), D = (1, 6)
1)
|AB|=
√32+72=
√58
|CD|=
√62+142=
√36+196=
√232=
√4*58=2
√58
k=−2
2)
środek jednokładności
z definicji jednokładności:
SC
→=k*SA
→
S=(x,y)
SC
→=[7−x, −8−y]
SA
→=[−2−x,3−y]
7−x=−2*(−2−x) i −8−y=−2*(3−y)⇔
============
26 kwi 23:11
xD: Dziękuję, tylko mam jedno pytanie licząc skalę wychodzi liczba dodatnia, ale w treści jest
założenie, że skala jest mniejsza od zera.
To można po prostu do obliczonej skali dać znak minusa? Czy istnieje sposób na dostanie ujemnej
skali przez obliczenia?
27 kwi 00:32
Eta:
w treści masz k<0 to k= −2
27 kwi 00:48
 C = (7, −8), D = (1, 6)
1)
|AB|=√32+72=√58
|CD|=√62+142=√36+196=√232=√4*58=2√58
C = (7, −8), D = (1, 6)
1)
|AB|=√32+72=√58
|CD|=√62+142=√36+196=√232=√4*58=2√58