geometria analityczna olek: Wyznacz liczbę elementów zbioru A ∩ B w zależności od parametru m, jeśli A={(x, y): y−x²+4x=3} i B = {(x, y): y – |x – 2| – m = 0}.

iteRacj@: A/ y−x²+4x=3 → y=x²−4x+3 B/ y−|x−2|−m=0 → y=|x−2|+m Sprzwdź, ile rozwiązań ma układ tych dwóch równań w zależności od parametru m.

olek: narysowałem te funkcje gdy m=0 lecz jest problem, bo.. 3 rozwiązania gdy m=0 2 rozwiązania gdy m>0 ale też ma 2 rozwiązania gdy funkcja kwadratowa B ma wierzchołek tuż pod funkcją A jak to zrobić?

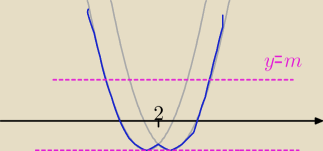
iteRacj@: przekształcamy x²−4x+3=|x−2|+m x²−4x+3−|x−2|=m 1/ dla x≥2 |x−2|=x−2 f(x)=x²−4x+3−x+2=x²−5x+5

−b
	=2,5 → postać kanoniczna f(x)=(x−2,5)2−1,25
2a

2/ dla x<2 |x−2|=−x+2 f(x)=x²−4x+3+x−2=x²−3x+1

−b
	=1,5 → postać kanoniczna f(x)=(x−1,5)2−1,25
2a

dla m<−1,25 brak rozwiązań m=−1,25 dwa rozwiązania −1,25<m<−1 cztery rozwiązania m=−1 trzy rozwiązania m>−1 dwa rozwiązania