matura unik: Trójkąt równoboczny ABC o boku a wpisano w okrąg. Na łuku BC wybrano punkt D tak, że proste AB i CD przecinają się w punkcie E i |BE| = 2a. Obliczyć pole S czworokąta ABCD i wykazać, że S =0,25*√3(BD+CD)²

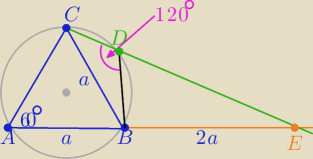
Eta: Czworokąt ABCD opisany na okręgu to <CDB=120^o P(ABCD)=S=P(ABC)+P(CBD)

	a2√3		1		√3
P(ABC)=		i P(CBD)=		*|CD|*|BD|*sin120o =		|CD|*|BD|
	4		2		4

z tw. cosinusów w ΔCBD a²=|CD|²+|BD|²−2|CD|*|BD|*cos120^o a²=|CD|²+BD|²+|CD|*|BD|

	√3
S=		*(a2+|CD|*|BD|)
	4

	√3
S=		(|CD|2+2|CD|*|BD|+|BD|2)
	4

	√3
S=		(|BD|+|CD|)2
	4

==================

Eta: Poprawiam zapis : czworokąt ABCD jest oczywiście wpisany w okrąg