Zadanie optymalizacyjne (bryła wpisana w bryłę). Czy rozwiązuję je dobrze? Miszka: Cześć, czy moglibyście proszę sprawdzić zadanie, które sobie rozwiązuje? Niestety w pewnym momencie wychodzi mi straszna głupota (pole walca równe 0) i nie wiem, czy błąd jest w obliczeniach czy w założeniach. Treść zadania i moje obliczenia dodaję poniżej. Z góry dziękuję! Zadanie: Rozważmy zbiór wszystkich walców wpisanych w kulę o promieniu R. Znajdź wymiary tego walca, który ma największą objętość. 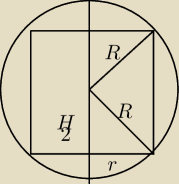Narysowałem sobie powyższy rysunek (przepraszam, że taki brzydki). Oznaczenia − R (promień kuli), r − promień podstawy walca, H/2 − połowa wysokości walca. Z Pitagorasa wyliczam długość H/2 − wzór będę uzależniał od r. Mam: R² − r² = 1/4 h² 4R² − 4r² = h² H = √4R² − 4r² Wprowadzam wzór na objętość walca: V = πr²h = πr²√4R² − 4r² Stąd: V(r) = √4R²π²r⁴ − 4π²r⁶ Jako, że funkcja jest pod pierwiastkiem, to wyciągam ją pomocniczo. Piszę komentarz o monotoniczności, miejscach zerowych itp... f(r) = 4R²π²r⁴ − 4π²r⁶ = 4π²r⁴(R² − r²) No i wychodzi zły wynik. Czy gdzieś tu robię błąd? Czy źle wyciągam tę funkcję? Proszę o jakąś radę.

Miszka: Tyle się napisałem, a okazało się, że źle policzyłem pochodną... O ironio!

ICSP: