Wielomiany. Rozwiąż nierówność. Grześ: Wielomiany. Rozwiąż nierówność. Proszę o pomoc, bo mam duży problem z tymi podpunktami. a) |x² − 2x| ≥ x³ b) |x³ − 8| > x² + 2x +4 c) √x⁴ − x² ≤ 4−x²

Jerzy: a) Dla : x² − 2x ≥ 0 masz nierównośc: x² − 2x − x³ ≥ 0 Dla : x² − 2x < 0 masz nierównośc: − x² + 2x − x³ ≤ 0 i działaj.

Grześ: https://drive.google.com/file/d/1Exs4n5QBGdlM_qAHa-IpN2dBj_G3Mz0m/view?usp=sharing aktualny moment wykonania podpunktu w linku, jak teraz wykonać wężyk? drugie pytanie, nie powinno być "Dla : x² − 2x < 0 masz nierówność: − x² + 2x + x³ ≤ 0"

Jerzy: Nie, bo wartość bezwzgledna nie dotyczy jednomianu x³. Prawidłowe rozwiązanie: x ∊ (−∞,1]

ZKS: Jeżeli rozbijamy na przypadki to: dla x² − 2x ≥ 0 dostaniemy nierówność x² − 2x ≥ x³ dla x² − 2x < 0 otrzymamy nierówność −(x² − 2x) ≥ x³. Można również zrobić w ten sposób. Dla x < 0 mamy rozwiązanie tej nierówności, natomiast dla x ≥ 0 nierówność przyjmuje postać. x² − 2x ≥ x³ ∨ x² − 2x ≤ −x³.

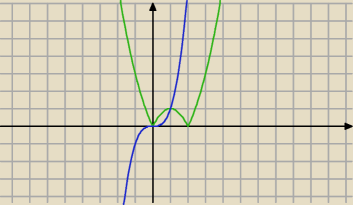
Jerzy: Rozwiązanie graficzne.