Prosze o pomoc Wwo: Dane są równania okręgów K1 : (x − 4)² + y² = 9 i K2 : (y − 3)² + x² = 9. Napisz równania wspólnych stycznych do tych okręgów.

Wwo: Ktoś ma pomysł od czego zacząć?

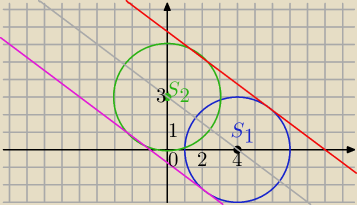
Mila: K1 : (x − 4)² + y² = 9, S₁=(4,0), r=3 i K2 : x²+(y − 3)² = 9, S₂=(0,3) r=3 1) Styczne będą równoległe do prostej S₁S₂

	3
k: y=ax+3 i 0=a*4+3, a=−
	4

	3
y=−		x+3
	4

2) Styczne :

	3
y=−		x+b ⇔
	4

3x+4y−4b=0 Odległość stycznej od środka okręgu jest równa promieniowi

	|3*0+4*3−4b|
d(s,S2=(0,3))=		=3
	√32+42

|12−4b|=15 12−4b=15 lub 12−4b=−15

	3		27
b=−		lub b=
	4		4

	3		3
s1: y=−		x−		⇔3x+4y+3=0
	4		4

lub

	3		27
s2: y=−		x+		⇔3x+4y−27=0
	4		4

======================

Wwo: Dziękuję bardzo

Mila:

Wwo: A mogę liczyć na podpowiedź do tego zadania : K1 : (x − 4)² + y² = 9 i K2 : (y − m)² + x² = m². Okrąg K2 przecina oś OY w początku układu współrzędnych i punkcie C, a okrąg K1 przecina oś OX w punktach A i B. Oblicz pole czworokąta, którego wierzchołkami są punkty A, B, C i środek okręgu K2.

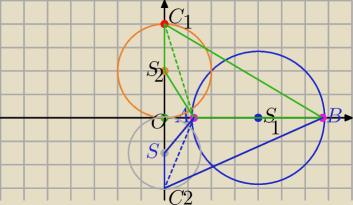
Mila: A=(1,0), B=(7,0) m>0, S₂=(0,m) C₁=(0,2m) Pole liczysz jako sumę dwóch Δ.

	1		1
P=		*6*2m+		*m*1
	2		2

dla m<0 ( K₂ na dół)

	1		1
P=		*6*2|m|+		*|m|*1
	2		2

Wwo: Jeszcze raz dziękuję, jesteś niesamowita