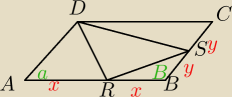
planimetria salv: Punkty R i S są środkami boków odpowiednio AB i BC równoległoboku ABCD. Wykaż, że pole

	3
trójkąta RSD jest równe		pola tego rownolegloboku.
	8

	3
PΔRSD=		PABCD
	8

P_ABCD=4xysinβ=4xysin(180−α)=4xysinα P_ΔADR=xysinα P_ΔDSC=xysinα

	xysinα
PΔRSB=
	2

	3
PΔRDS=		xysinα
	2

PΔRDS		3   2		3
	=		=		c.n.w
PABCD		4		8

i tu moje pytanie,czy da sie to zrobic jakos inaczej z podobienstwa?bo tak sie zastanawiam jakbym to zrobil inaczej nie znajac wzorow na pole Δ z sinusem i nic jak na razie mi do glowy nie przychodzi

salv: zle sie wyrazilem,po prostu jak to zrobic inaczej niekoniecznie z podobienstwa

jc: Trójkąty po bokach mają 1/4, 1/4, 1/8 pola całości. Sam łatwo uzasadnisz. W środku zostaje 1−1/4−1/4−1/8=3/8.

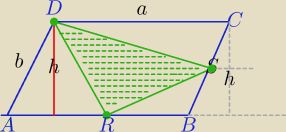Mila: 1) P{ABCD}=a*h ten wzór znasz! 2)

	1		1		1
PΔARD=		*		a*h=		a*h
	2		2		4

	1		1		1
PΔDCS=		a*		h=		a*h
	2		2		4

	1		1		1		1
PΔRBS=		*		a*		h=		a*h
	2		2		2		8

	1		1		3
3) PΔDRS=a*h−(		a*h+		a*h)=		a*h
	2		8		8

	3   ab 8		3
4)		=
	ab		8