okregi miki: Środki trzech stycznych okrągów połączono ze sobą tworząc trójkąt o bokach 6, 10 oraz 14. Oblicz odleglość AO, gdzie O środek najmniejzego okręgu stycznego do trzech pozostałych, a A wierzchołek trójkąta (patrz rys) https://i.stack.imgur.com/D7UPx.png

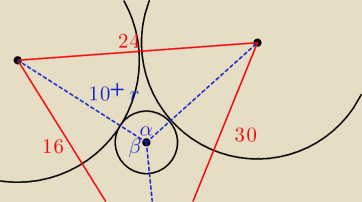
wredulus_pospolitus: z tw. cosinusów: 24² = (10+r)² + (14+r)² − 2(10+r)(14+r)cosα 16² = (10+r)² + (6+r)² − 2(10+r)(6+r)cosβ 30² = (6+r)² + (14+r)² − 2(6+r)(14+r)cos(180 − (α+β)) trochę pitolenia będzie ... ale masz układ trzech równań z trzema niewiadomymi ... więc można wyliczyć

miki: Skąd te liczby 24, 16 i 30?

wredulus_pospolitus: ach ... to już sa boki ... wartości 6,10,14 traktowałem jako promienie okręgów no to na początek wyznacz promienie tych trzech okręgów

miki: A jak wyzczyć te promienie?

wredulus_pospolitus: a < b < c a + b = 6 a + c = 10 b + c = 14 taki prosty układ

wredulus_pospolitus: uprzedzając pytanie: "skąd wiem że tak mają wyglądać równania" skoro a < b < c (tak sobie zakładam zmienne) to suma dwóch najmniejszych liczb (a i b) będzie najmniejsza (czyli = 6) to suma dwóch największych liczb (b i c) będzie największa (czyli =14) więc suma a i c będzie równa 10