okrąg matma: Na okręgu obrano trzy różne punkty X,Y,Z Styczne w punktach X i Y przecinają się w punkcie A , zaś styczna w punkcie Z przecina prostą XY w punkcie C Wykaż,że |AB|²=|AY|²+|BZ|²

ite: Gdzie jest pkt B?

ifka: wsakzówka − wez środkiem odcinka oznacz P i wtedy masz trojkąt prostokątny APC

ifka: Wg mnie to powinno być AC²=AY²+CZ² ?

matma: Tak, przepraszam |AC|²=|AY|²+|CZ|²

ifka: Powtarzam − wez środkiem odcinka XY oznacz P i wtedy masz trojkąt prostokątny APC. Bez gotowca

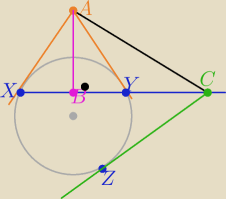
Eta: B −− środek odcinka XY to BY=BX z tw. Pitagorasa w ΔABC i w ΔABY AC²=BC²+AB² i AB²=AY²−BY² AC²=BC²−BY²+AY² AC²=(BC−BY)(BC+BY)+AY² AC²= CY*CX+AY² i z tw. o stycznej i siecznej CY*CX=CZ² to AC²=CZ²+AY² ============= c.n.w.

ifka: Eta nie dałes sie mu/jej nawet zastanowic

Eta:

ifka: Są tu inne zdania bez wskazówek nawet ale ok

jc: ... lub bez twierdzenia. AC² = BC² + AB² = (CS² − BS²) + (AY² − BY²) = CS² + AY² − (BS² + BY²) = AY² + CS² − r² = AY² + CZ² S = środek okręgu, r − promień