Zbadaj ciągłość funkcji Limes: Zabrałem się za zagadnia związane z granicami, pochodnymi i tym podobne. Jednak nie do końca mogę zweryfikować czy wszystko dobrze rozumiem (strajk nauczycieli ). Dlatego przychodzę z prośbą o pomoc. Przedstawię dwa zadania związane z granicami i bezpośrednio z ciągłościami funkcji. Zacznijmy od zadania: Uzasadnij, że funkcja f(x) = −2x³ + x² − 3x + 2 ma miejsce zerowe należące do przedziału <0; 1> Rozpatrzyłem to w taki sposób: lim x → 1⁻ = [−2 + 1 − 3 + 2] = −2 lim x → 0⁻ = [0 + 0 − 0 + 2] = 2 Granice te przyjmują wartości przeciwne − będące po przeciwnej stronie osi odciętych. Znaczy to, że w pewnym momencie jako, że funkcja jest ciągła musi przeciąć oś odciętych w tym przedziale <0; 1> I drugie zadanko, które zupełnie nie mam pojęcia jak rozwiązać

	⎧	−x2 dla x ∊ <−1;1>
Zbadaj ciągłość funkcji f(x) =	⎨
	⎩	x−1|x−1| dla x∊(−∞; −1)∪(1;+∞)

Na pewno wiem, że dla lim x→_−1⁻ mianownik przyjmie wartość −x+1 a dla lim x→_1⁺ przyjmie wartość x−1 Jednak przyznam się, że po prostu nie do końca wiem jak to ugryźć ._. Przepraszam, troszkę tego nie widzę i do końca nie wiem co liczę... Mam nadzieje, że troszkę rzucicie mi na to światło ;−;

Limes: Tam wdarł się mały błąd w pierwszym zadaniu, gdzie lim x →_0⁻ powinien właśnie zbiegać z prawej strony, czyli lim x →_0⁺

ICSP: https://pl.wikipedia.org/wiki/W%C5%82asno%C5%9B%C4%87_Darboux − masz odpowiedx na pierwsze. Nie musisz brać granic, wystarczy wziąc wartości w punkcie (f. jest ciągła). f(a) * f(b) < 0 ⇒ istnieje c ∊ (a , b) takie, że f(c) = 0. Jednak wypada najpierw napisać, ze wielomian jest funkcją ciągłą. W końcowym wniosku powołać się na własność Darboux.

ICSP: Co do drugiego. Zacznij od jednego punktu. Masz sprawdzić czy lim_{x → x0⁻} = f(x₀) = lim_{x → x0⁺}

wredulus_pospolitus: zadanie 1 Zbyteczne jest liczenie granic w sytuacji, gdy funkcja jest ciągła w przedziale <0;1>. Skorzystaj z tw. Darboux (https://pl.wikipedia.org/wiki/Twierdzenie_Darboux) czyli: jeżeli funkcja jest ciągła na przedziale [a,b] oraz f(a)*f(b) < 0 (czyli wartości funkcji są różnych znaków) to ∃_c∊(a,b) f(c) = 0 (istnieje punkt c ∊ (a,b) dla którego f(c) = 0)

Stado ślimaków: a nie możesz w pierwszym zadaniu po prostu obliczyć f(0) i f(1) , dlaczego granice liczysz? a w drugim rozpisz z definicji wartości bezwzględnej i ten ułamek będzie równy albo 1 albo −1

wredulus_pospolitus: zadanie 2

	x−1		x−1
limx−>−1− f(x) = limx−>−1−		= limx−>−1−		= −1
	|x−1|		−(x−1)

	x−1		x−1
limx−> 1+ f(x) = limx−> 1+		= limx−> 1+		= 1
	|x−1|		x−1

inny granic NIE TRZEBA liczyć bo: f(−1) = −(−1)² = −1 f(1) = −(1)² = −1

Limes: Bardzo dziękuje za rady, będę musiał sobie to wszystko na spokojnie przyswoić − szczególnie jak wstanę, bo już dopada mnie zmęczenie. Zadanie pierwsze chyba rozumiem, a zadanie drugie....funkcja nie jest ciągła ponieważ na swój sposób jest ciągłość jest przerwana w punkcie f(1), tak? Wartość tam jest −1, a granica dąży do 1

Jerzy: Funkcja jest ciągła w punkcie, gdy posiada wartość w tym punkcie i istnieje granica w tym punkcie równa wartosci funkcji w tym punkcie.

Limes: Okej, dziękuje! To też oznacza, że takich funkcji, które nie są ciągłe moge się spodziewać właśnie w takich równaniach z podanymi przedziałami, a samego sprawdzenia czy funkcja jest ciągła powinienem dokonywać na końcach/początkach tych przedziałów, tak?

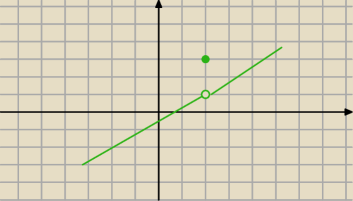
Jerzy: Tak. W punktach styku takich przedziałów.Tutaj masz przykład funkcji nieciągłej w punkcie x = 2. Granca wynosi 1 , ale wwartośc funkcji 3

Limes: Dziękuje! W końcu czuje, że rozumiem

Adamm: Tw. Darboux jest bezpośrednim wnioskiem z faktu, że obraz zbioru spójnego przez funkcję ciągłą jest spójny

jc: Chyba raczej twierdzenie Bolzano. https://en.wikipedia.org/wiki/Intermediate_value_theorem Jest podobne twierdzenie Darboux, ale dotyczy pochodnych https://en.wikipedia.org/wiki/Darboux%27s_theorem_(analysis)