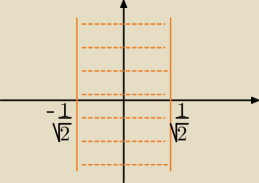
przeciwobraz zbioru iteRacj@: Dana jest funkcja f: ℛ✖ℛ → ℛ✖ℛ i zbiór B⊆ℛ✖ℛ . Naszkicuj w prostokątnym układzie współrzędnych zbiór f⁻¹[B] 1/ B={<x,y>∊ℛ✖ℛ: x²+y²=1}

	−1		1
Czemu w odpowiedziach ten pas wyznaczają proste x=		i x=		a nie x=−1 i x=1 ?
	√2		√2

Basia: no a gdzie ta funkcja? i co to jest 1/ B?

iteRacj@: Witaj Basiu : ) zgubiłam wzór funkcji f(x,y)=<x,x> 1/ to podpunkt pierwszy

Basia: f(C) dało nam okrąg x²+y²=1 czyli szukamy takich x, dla których x²+x² = 1

	1
no to x = ±		a y dowolne
	√2

iteRacj@: Dziękuję!

Basia: ale dla x²+y²=1 to nie jest pas tylko te dwie proste pas dostaniesz dla x²+y²≤1

iteRacj@: Sprawdziłam jeszcze raz: w treści na pewno jest x²+y²=1, a w odpowiedzi jest pas a nie proste.

Basia: weź parę z tego pasa, ale nie z żadnej z tych prostych np. (0,2) f(0,2) = (0,0) 0²+0² z całą pewnością ≠ 1 czyli f(pasa) ≠ B

iteRacj@: Już rozumiem, dzięki za wytłumaczenie.

Basia: ale coś mi się jeszcze nie zgadza jeżeli f(x,y)=(x,x) to do każdego zbioru wartości będą należały tylko pary o takich samych współrzędnych do zbioru B należą nie tylko takie pary i tu mi coś zgrzyta

Basia: czy może źle odczytałam zapis funkcji? <x,x> to para współrzędnych czy może coś innego?

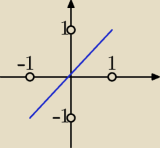
iteRacj@: <x,x> to para współrzędnych W tym zadaniu jest jeszcze jedna część polecenia. Zrobiłam je i wynik mam zgodny z odpowiedziami, więc go nie wpisałam. Ale może ono coś jeszcze wyjaśni. Naszkicuj w prostokątnym układzie współrzędnych zbiór f[A]: dla A={<x,y>∊ℛ✖ℛ: x²+y²=1} /taki sam jak B z 22:23/ Jest to okrąg o środku (0,0) i promieniu 1 → x∊<−1,1> → f[A] to zbiór punktów o obu takich samych współrzędnych o wartościach z przedziału <−1,1>. Czy to się zgadza?

Basia: tak, to się zgadza, ale równocześnie potwierdza to co napisałam wcześniej zbiór B czyli okrąg nie może być zbiorem wartości tej funkcji należą do niego punkty np. (−1,0) (0,1) itp., które wartościami tej funkcji być nie mogą w B są tyko dwa punkty postaci (x,x); (−1/√2,−1/√2) i (1/√2,1/√2)

ite: Wieczorem jeszcze raz spokojnie to przemyślę.