maturalne Twój: Wyznacz zbiór wszystkich punktów P=(a;b) płaszczyzny, jeśli wiadomo, że a i b są wartościami parametru przy których równanie a ⁴x ³−3a ²x+b=0 ma dokładnie 3 różne pierwiastki rzeczywiste.

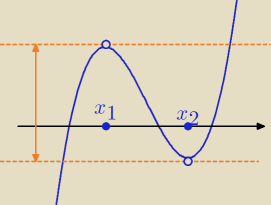
iteRacj@: a⁴≠0 1/ Wyznacz f.pochodną f(x)=a⁴x³−3a²x+b f'(x)=3a⁴x²−3a² 2/ Znajdź wartości parametru a, dla których f(x) ma dwa ekstrema lokalne 3a⁴x²−3a²=0 3a²(a²x²−1)=0 3/ Ustal, dla jakich wartości parametrów f(x₁)>0 i f(x₂)<0 / ← sytuacja na rysunku/

Twój: czyli x₁=1/a oraz x₂=−1/a i co dalej?

iteRacj@: Obliczamy f(x₁) i f(x₂).

iteRacj@: Zakładamy, że a>0. Wtedy dla x₁ funkcja ma maksimum lokalne i dla x₂ ma minimum. (Można też założyć, że a<0 wtedy ekstrema są odwrotnie)

ICSP: Nie będą odwrotne. Zresztą nie interesuje nas czy wcześniej występuje minimum czy maksimum. Chcemy aby ekstrema były różnych znaków, więc warunek : f(x₁) f(x₂) < 0 gdzie x₁ , x₂ są miejscami zerowymi pochodnej, jest wystarczający.

iteRacj@: I tak pokręciłam...

Twój: czyli wyszło (−2a+b)(2a+b)<0

iteRacj@:

	−1		1
Ja mam f(		)=−4a+b i f(		)=−2a+b.
	a		a

Twój: Dzieki a jak to narysoawć teraz (−4a+b)(−2a+b)<0

ICSP:

	1		b
f(x) = x3 − 3		x +
	a2		a4

	1		b2
Δ = −		+		< 0 ⇒ −4a2 + b2 < 0 ⇒ (b − 2a)(b + 2a) < 0
	a6		4a8

Przy założenia a ≠ 0

ICSP: Czyli mamy 2 proste: b = 2a i b = −2a które dzieją R² na 4 części. Wystarczy zaznaczyć odpowiednie obszary.

Twój: A które to będą obszary?

ICSP: Wybierz dowolny punkt z każdego z 4 obszarów i podstaw do nierówności (b − 2a)(b + 2a) Jak będzie spełniona to kreskujesz dany obszar. Sposób z podstawówki ale bardzo skuteczny.