figury Kuba: Zadanie maturalne Na ostrosłupie prawidłowym trójkątnym opisano stożek, a na tym stożku opisano kulę. Kąt przy wierzchołku przekroju osiowego stożka jest równy α. Dla jakiej wartości α stosunek objętości kuli do objętości ostrosłupa jest najmniejszy?

wredulus_pospolitus: A w jaki sposób tenże stożek jest opisany na tym ostrosłupie?

Kuba: Tak jest treść ale wg mnie trojkąt jest wpiasny w okrąg dolny, a wierzchołek ostrosłupa jest w srodku okręgu górnego.

Basia: podejrzewam, że podstawa na podstawie, a wierzchołek wspólny

Basia: jakiego okręgu górnego? to stożek ma być, a nie walec

wredulus_pospolitus: Basiu ... zapewne tak ... ale nie jest to 'jedyny sposób' na opisanie stożka na ostrosłupie

wredulus_pospolitus: a że mam nastrój na 'czepianie' się ... to się czepiam

Basia: oj wiem, tylko te wszystkie inne to już kosmos

Kuba: No tak sorry w stożek To zadanie było kiedyś na maturze

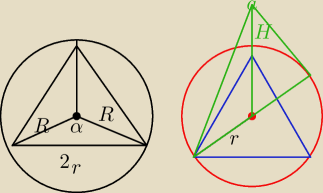
Basia: po lewej kula i stożek (2r)²=R²+R²−2*R*R*cos α 4r² = 2R²(1−cos α)

	2r2		2r2		r2
R2 =		=		=
	1−cos α		2sin2 α/2		sin α/2

	r
R =
	sin α/2

	r
tg (α/2) =
	H

	r
H=
	tg α/2

	2h		2a√3		a√3
r =		=		=
	3		2*3		3

a = r√3

Vo		1   r2*3*√3   r   * * 3   4   tg α/2
	=		=
Vk		4   r3   π* 3   sin3 α/2

r3*3√3*sin3 α/2		3√3*sin3 α/2*cos α/2
	=		=
16πr3*tg α/2		16π*sin α/2

3√3
	*sin2 α/2 * cos α/2
16π

no i teraz trzeba znaleźć minimum f(α)=sin² α/2 * cos α/2 przy założeniu α∊(0^o; 180^o) to już potrafisz? a poza tym posprawdzaj te rachunki, mogłam się pomylić

Kuba: A tam nie piwnno być V_k/V_o ?

Kuba: i chyba tam ta 16 jest nieptrzebna?

Basia:

	1		4		1
potrzebna		/		=
	3		3		4

Basia: powinno być V_k/V_o; trzeba odwrócić

Kuba: Czyli jaka jest osateczna odpowiedz? bo już się pogubiłem

Basia: no nie; trzeba teraz szukać minimum

Kuba: A jak to minimum znaleźć?

Basia: Tam jest błąd na samym początku i w ogóle można w prostszy sposób to zrobić. Napiszę dokładne trochę później.

Kuba: Ok czekam....

Nauczyciel: Nie czekaj matury nie bedzie ! ! !

Kuba: kiedys tam bedzie......

6latek: Spokojnie . matury sie odbeda . Jesli by sie mialy nie odbyc to we wrzesniu nauczyciele do konca straca autorytet .

Kuba: A może ktoś z tym zadanie pomóc?

Mila: Piszę, cierpliwość wskazana

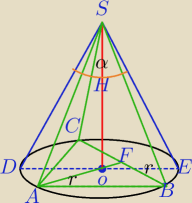
Mila: 1) α∊(0,π)

	α		r		α
W ΔSOE: sin		=		⇔r=l*sin
	2		l		2

	α		H		α
cos		=		⇔H=l*cos
	2		l		2

2) ΔABC− Δrównoboczny,AO|=r− promień podstawy stożka

	3		a√3
h=|AF|=		r=		⇔3r=a√3⇔
	2		2

	3r
a=		=r√3
	√3

	1		1		(r√3)2*√3		α
3) VABCS=		*PΔABC*H=		*		*lcos		⇔
	3		3		4		2

	√3		α   α   3*l2sin2 *l*cos   2   2
VABCS=		*		=
	3		4

	√3		α		α
=		*l3*sin2		*cos
	4		2		2

====================== 4) W ΔDES:

2r
	=2R
sinα

	r
R=
	sinα

	4π		4π		r		4π		α   l3*sin3   2
Vkuli=		*R3=		*(		)3=		*
	3		3		sinα		3		sin3α

	4π		α   l3*sin3   2
Vkuli=		*		=
	3		α   α   8*sin3 *cos3   2   2

	π		l3
=		*
	6		α   cos3   2

==================== Teraz sprawdzaj ten fragment z odpowiedzią, będę na forum po 20

Kuba: Tak bo na innym forum jest to zadanie wiec odpwiedz na razie taka sama ale nie ma wyznaczonego tego najmniejszego α

Mila: 5) α∊(0,π)

	vk		πl3		4
s(α)=		=		*
	Vo		α   6cos3   2		α   α   √3*l3*sin2 *cos   2   2

	2√3π		1
s(α)=		*
	9		α   α   sin2 *cos4   2   2

S(α) ma najmnieszą wartość, jeżeli mianownik osiągnie największą wartość.

α

α

α

α

α

α

f(α)=(sin2

*cos4

)=(1−cos2

)*cos4

=cos4

−cos6

2

2

2

2

2

2

	α		1		α		α		1
f'(α)=4cos3α*(−sin		)*		−6cos5		*(−sin		)*
	2		2		2		2		2

	α		α		α		α
f'(α)=−2sin		*cos3		+3sin		*cos5
	2		2		2		2

	α
f'(α)=0⇔3 cos2		−2=0, cosα>0
	2

	α		√6
cos		=
	2		3

α≈70^o nie wiem, czy nie ma pomyłki, bo wydawało mi się ,że to będzie inny kąt.

Mila: Pytają o kąt α, to można wyrazić odpowiedź za pomocą cosinusa α.

	α		1+cosα
cos2		=
	2		2

2		1+cosα
	=
3		2

4
	=1+cosα
3

	1
cosα=
	3

To jest dobra odpowiedź. Zadanie maturalne z 1994 roku.