. mod: Jak sprawdzić położenie prostej względem okręgu? Dokładnie chodzi o okrąg x²+y²=36 i prostą x−2y+5=0

wredulus_pospolitus: można np. graficznie

wredulus_pospolitus: II sposób: wyznaczasz odległość punktu (środka okręgu) od danej prostej (w tablicach masz odpowiedni wzór)

wredulus_pospolitus: III sposób rozwiązujesz układ równań:

⎧	x2 + y2 = 36
⎩	x−2y+5 =0

mod: dziękuję bardzo

wredulus_pospolitus: chociaż akurat ta prosta 'tak ewidentnie' przecina tenże okrąg, że aż wstyd byłoby stosować II lub III sposób. wystarczy odczytać 'najprostsze' punkty prostej (punkt przecięcia się z osią OX oraz OY) i porównać to z promieniem okręgu, aby zauważyć że oba (a wystarczy że jeden z nich) te punkty leżą wewnątrz okręgu

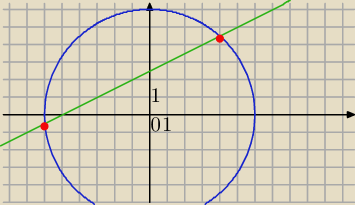
iryt: x²+y²=36 i prosta k: x−2y+5=0, x=2y−5 S=(0,0), r=6 1) sposób Odległość prostej od środka okręgu:

	|0−2*0+5|		5
d(S,k)=		=		=√5
	√1+4		√5

√5<6⇔ prosta ma dwa punkty wspólne z okręgiem albo tak: 2) Zbadać ile rozwiązań ma równanie: (2y−5)²+y²=36⇔ y=2−√³¹₅ lub y=2+√³¹₅ x=−1−2√³¹₅ lub x=−1+2√³¹₅ Dwa punkty wspólne