czworokat Mira: O czworokacie ABCD wiadomo ze AB=2, AD=4, ∡ABC jest prosty, ∡BCD=78^o oraz ∡BAD=∡ADC. Wyznacz ∡CAD.

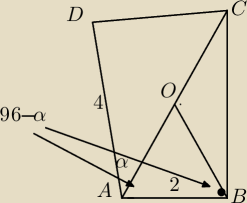
a7: obliczamy kąt BAD=ADC=96 gdyż suma miar kątów w czworokącie jest 360 wyznaczamy środek odcinka AC (gdyż trójkąt ABC jest prstokątny i można na nim opisać okrąg) i mamy trójkąt równoramienny ABO gdzie kąt przy podstawie AB jest równy 96−α a kąt przy wierzchołku równy 180−(2(96−α))=2α−12, z trójkąta równoramiennego BCO mamy kąt przy wierzchołku równy ∡BOC=180−(2α−12)=192−2α

	192−2α
kątOBC równa się		=96−α
	2

kąt ABC jest 90 i jest sumą kątów ABO i OBC 96−α+96−α=90 czyli α=51

a7: nie jednak źle, sorry

miki: Wg mnie to 24^o ale za dużo liczenia

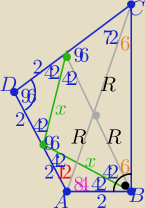
Eta: |<CAD|=12^o

Hugo: Eta a ile wynosi ACB?

Mira: Nic nie rozumiem z tego rysunku

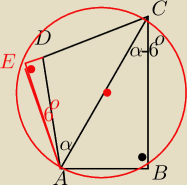
an: EA=4cos6

4cos6		2
	=
sin(84−α)		sin(α−6)

α=30^o

Mira: Co to za punkt E?

an: E to punkt przecięcia przedłużenia odcinka CD z prostopadłą do niego przechodzącą przez wierzchołek A

an: Dzieki temu na czworokącie ABCE można opisać okrąg, a AC jest średnicą tego okręgu, Kąty A i E są kątami prostymi.

miki: an a ACB=24^o

an: DAC=α=30° ,kąty B i E proste, jak zaznaczone na rysunku.

miki: Ale ja się pytam o ACB?

an: ACB=α−6=24, pisze z komórki i niezbyt dobrze mi to wychodzi